Замены

Понятие формального предиката. Замена элементарной формулы формальным предикатом (индуктивное определение). Теорема о замене элементарных подформул. Правило замены эквивалентным. Пример: эквивалентность r(x)∨∀z(¬∀xq(x,z)) и r(x)∨∀z(∃x¬q(x,z)). Принцип двойственности. Нильпотентность. Эквивалентность двойственных формул.

Речь идет о получении аналога теоремы 2.3. У нас нет самостоятельных пропозициональных переменных. Их роль играют предикатные символы арности нуль. Разумеется, теорема 2.3 остается верной при замене предикатного символа арности нуль какой-либо формулой. Но как быть, если нужно заменить предикатный символ, имеющий параметры? Таким образом, речь идет об обобщении теоремы 2.3 на случай замены в формуле произвольной элементарной подформулы. Механизм замены должен сохранять эквивалентность формул.

При замене какого-либо вхождения элементарной подформулы p(t₁,...,t_n) (аргументы в этой подформуле — какие-либо термы) некоторой формулой X следует установить соответствие между переменными, входящими в элементарную подформулу, и переменными, входящими в X. Такое соответствие можно организовать, вводя понятие формального предиката. Под формальным предикатом мы будем понимать слово вида x₁x₂ ...x_nX. Такое слово означает лишь, что задана какая-то формула X и упорядоченный набор переменных x₁, x₂, ..., x_n — больше ничего. Эти переменные и все их вхождения в X в рамках формального предиката будем считать связанными. Кортеж сортов (π₁, π₂, ..., π_n) " объявленных" переменных x₁, x₂, ..., x_n будем называть типом формального предиката.

Чтобы в формуле Y заменить элементарную подформулу p(t₁,...,t_k), необходимо построить формальный предикат U = x₁x₂ ...x_nX того же типа, что и предикатный символ p, затем в формуле X выполнить подстановку X^{x1,...,xnt1,...,tn} и результат подстановки подставить в формулу Y взамен подформулы p(t1,...,pn).

Подобный подход будет более понятным, если учесть, что в любой модели формула задает предикат, роль аргументов которого играют переменные формулы. Задавая формальный предикат, мы выбираем некоторую совокупность переменных (записываем их перед формулой) и упорядочиваем. Эти отобранные переменные фиксируются, остальные остаются свободными. При подстановке вместо элементарной формулы мы должны на место " объявленных аргументов" предиката подставить аргументы элементарной формулы и в таком виде подставить формулу вместо элементарной. Например, пусть элементарная формула имеет вид p(t1,t2,...,tn). Формальный предикат x₁x₂ ...x_nX следует в любой модели интерпретировать как предикат p˜(x₁,...,x_n,z₁,...,z_m), в котором первые n аргументов по типам соответствуют аргументам предиката p. В результате мы меняем в исходной формуле элементарную подформулу p(t₁,t₂,...,t_n) на подформулу p˜(t₁,...,t_n,z₁,...,z_m). Отобранные элементы формального предиката играют роль подстановочных мест и заменяются аргументами элементарной подформулы. Оставшиеся переменные формулы X без изменений переходят в изменяемую формулу.

Указанный алгоритм подстановки можно описать с помощью индукции по построению формулы. Пусть задан формальный предикат U = x₁x₂ ...x_nX и Y обозначает исходную формулу. Результат Y (p||U) подстановки в Y формального предиката U типа (π₁, π₂, ..., π_n) вместо элементарной подформулы p(t₁,...,t_n) с предикатным символом p того же типа определим следующим образом.

1. Если Y — атомарная формула q(r1,...,rm), то при q, отличном от p полагаем Y (p||U) = = Y , а если Y = p(t1,...,tn), то полагаем Y (p||U) = Xθ, где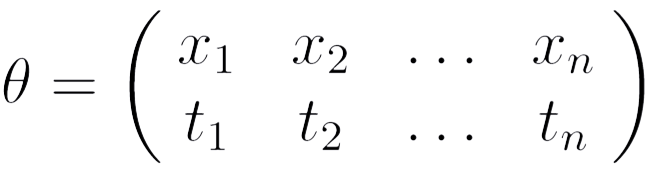

2. Если Y = V∇W, где ∇ — одна из трех двуместных логических связок, то Y (p||U) = = V (p||U)∇W(p||U). Если Y = ¬V , то Y (p||U) = ¬V (p||U).

3. Если Y = ∇z V , где ∇ — один из кванторов, то возможны два случая. В первом случае,когда U не содержит свободных вхождений z или V не содержит вхождений предикатного символа p, полагаем Y (p||U) = ∇z V (p||U). Во втором случае, когда z имеет свободные вхождения в U, а V имеет вхождения p, выбираем новую переменную u (т.е. не встречающуюся ни в Y , ни в U) и полагаем Y (p||U) = ∇u(V ^zu )(p||U).

Обратим внимание на то , что в соответствии с описанным индуктивным правилом при замене меняются все вхождения данного предикатного символа. Последний пункт регулирует вхождение свободных переменных формального предиката. Снова действует правило: никакое свободное вхождение переменной после преобразования не должно оказаться связанным. Если такое получается, соответствующую кванторную переменную надо изменить.

Теорема 4.3. Если X ≡ Y , то и X(p||x₁ ...x_kZ) ≡ Y (p||x₁ ...x_kZ). Если Y ≡ Z, то и X (p||x₁ ...x_kY ) ≡ X(p||x₁ ...x_kZ).

Первое утверждение сводится к следующему: если U — тавтология, то и U(p||x₁ ...x_kZ) — тавтология (достаточно в качестве U взять формулу X ~ Y ). То, что U — тавтология, означает, что при любой интерпретации и любой оценке формула U истинна. Интерпретация, в частности, обеспечивает конкретное содержание предикатного символа p, а формальный предикат x₁x₂ ...x_kZ превращается в некоторый предикат q(x₁,...,x_k,y₁,...,y_l). При замене происходит замена одного предиката другим, при этом появляются свободные переменные y₁, ..., y_l, которые мы можем зафиксировать с помощью оценки. В результате дело фактически сводится к замене предикатной буквы p на предикатную букву q. Такую замену можно интепретировать как изменение интерпретации буквы p. При изменении интерпретации формула остается истинной. Значит, и после замены формула остается истинной. Доказательство второго утверждения аналогично. Замена предикатного символа p одним из формальных предикатов можно интерпретировать как выбор интепретации символа p. Так как формулы Y и Z эквивалентны, то и первая, и вторая замены дают одну и ту же интерпретацию символу p. Следовательно и истинностное значение двух формул будет одинаковым.

Следствие 4.1. Если Y ≡ Z, то после замены в формуле X одного из вхождений подфор-мулы Y формулой Z получим формулу X', эквивалентную X.

Пусть x₁, x₂, ..., x_n — полный список переменных, входящих в формулы Y и Z. Рассмотрим формулу Γ, полученную заменой подформулы X элементарной формулой p(x₁,x₂,...,x_n). Тогда X = Γ(p||x₁ ...x_kY ) и X' = Γ(p||x₁ ...x_kZ). Согласно теореме эти формулы эквивалентны.

Утверждение следствия известно как правило замены эквивалентным.

Пример 4.3. Покажем, что формулы r(x)∨∀z (¬∀xq(x,z)) и r(x)∨∀z(∃x¬q(x,z)) эквивалентны.

Обе формулы можно рассматривать как две подстановки в формулу X = r(x) ∨∀z p(z) двух эквивалентных формул V = ¬∀xq(x,z) и W = ∃x¬q(x,z). Сформируем два формальных предиката zV и zW. В результате получим X(p||zV ) = r(x)∨∀z (¬∀xq(x,z)) и X(p||zW) = = r(x)∨∀z(∃x¬q(x,z)). В соответствии с последним логическим законом эти формулы эквивалентны.

Отметим, что было бы неверно в качестве шаблона использовать, например, формулу X₁ = = r(x)∨∀z p, опуская в заменяемом символе связанную переменную z. В этом случае в соответствии с индуктивным правилом мы получили бы формулы X₁(p||zV ) = r(x)∨∀z₁ (¬∀xq(x,z)) и X₁(p||zW) = r(x)∨∀z₁(∃x¬q(x,z)), которые тоже эквивалентны, но отличаются от того, что мы хотели бы получить.

На формулы алгебры предикатов, не содержащие импликации, распространяется принцип двойственности. Формулу X∗, двойственную данной формуле X определим индуктивно:

1) если X — элементарная формула, то X∗ = X;

2) если X = ¬U, то X∗ = ¬U∗;

3) если X = U ∧V , то X∗ = U∗∨V ∗;

4) если X = U ∨V , то X∗ = U∗∧V ∗;

5) если X = ∀xU, то X∗ = ∃xU∗;

6) если X = ∃xU, то X∗ = ∀xU∗.

Непосредственно из определения следует, что преобразование двойственности нильпотентно: X** = X. Следующее утверждение связывает преобразование двойственности с отношением эквивалентности. Крометого, верноследующееутверждение. Назовемвнутреннимотрицанием X^ˇ ; формулы X ее преобразование, при котором каждая элементарная подформула p(t₁,t₂,...,t_n) заменяется формальным предикатом x₁x₂ ...x_n¬p(x₁,x₂,...,x_n).

Если X = U ∧ V и уже доказано, что U* ≡ ¬ U^ˇ , V* ≡ ¬ V^ˇ , то согласно определению двойственной формулы и правилу замены эквивалентным

X* = U* ∨ V* ≡ ¬U^ˇ ∨ ¬V^ˇ ≡¬(U^ˇ ∧ V^ˇ ) = ¬X^ˇ .

Аналогичны рассуждения для кванторной приставки ∃x.

Теорема 4.5. Эквивалентность X ≡ Y равносильна эквивалентности X* ≡ Y* .

Доказательство в силу нильпотентности достаточно провести в одну сторону. При этом достаточно заметить, что если X ≡ Y , то X^ˇ ≡ Y^ˇ и ¬X ≡ ¬Y . Поэтому в силу предыдущей теоремы

X* ≡ ¬X^ˇ ≡ ¬Y^ˇ ≡ Y *.