Логические законы

Теория

Формулы общезначимые, выполнимые, опровержимые, тождественно ложные. Пропозициональные тавтологии. Тавтологии с кванторами. Пример: ¬∃x¬X →∀xX — тавтология; ∀x∃y p(x,y)→∃y∀xp(x,y) — нет. Основные логические законы: а) де Моргана (пронесение через отрицание); б) пронесение кванторов через бинарные связки (8 законов); в) обобщенное пронесение кванторов через дизъюнкцию и конъюнкцию (4 закона); г) добавление кванторов или изменение порядка (5 законов); д) законы конгруэнтности.

Среди формул языка Ω есть такие, которые остаются истинными при любой интерпретации и при любой оценке. Такие формулы называют тавтологиями или общезначимыми формулами. То, что X — тавтология, будем записывать так: |= X. Например, формула p → (q → p) истинна в любой модели, поскольку вообще не имеет параметров и в любой модели автоматически становится оцененной, тождественно истинной формулой. В то же время есть формулы, которые являются тождественно истинными для данной модели, но не являются тождественно истинными в другой модели. Например, формула x·y = y ·x в модели ω тождественно истинна. Однако, если в качестве модели взять множество квадратных матриц (операции x+ можно поставить в соответствие добавление единичной матрицы) с естественной интерпретацией двуместных функциональных символов, формула x · y = y · x уже не будет тождественно истинной. Если формула X является истинной в данной модели M при любой оценке (т.е. тождественно истинна в M), но не является истинной в некоторой другой модели при некоторой оценке, то эта формула выражает закон в модели M, истинность X в модели M будем обозначать M |= X.

Поскольку нульарные предикатные символы не имеют параметров, их значение не меняется в рамках заданной модели. Поэтому множество всех нульарных предикатных символов в сочетании с логическими связками образует подмножество рассматриваемого языка, идентичное языку алгебры высказываний. Следовательно, любой тавтологии из алгебры высказываний соответствует тавтология языка Ω. Например, |= ¬ A ∨ B → ¬(A ∧¬B), так как это калька с тавтологии из алгебры высказываний. Такие тавтологии будем называть пропозициональными. В них нет ни предметных переменных, ни кванторов.

Кроме пропозициональных тавтологий в языке Ω есть и другие тавтологии, порожденные кванторами. Например ¬∃x¬X →∀xX — тавтология. Чтобы это показать, выберем произвольную модель M и в ней произвольную оценку θ. Поскольку переменная x не входит свободно в X, можно считать, что x не входит и в θ. Проделаем подстановку по всем правилам в формуле. В результате придем к M | = ¬ ∃x ¬ (Xθ)→∀x (Xθ). Импликация связывает две оцененные формулы. Для доказательства ее истинности можно предположить, что левая часть импликации истинна, т.е. M |= ¬∃x¬(Xθ). Надо доказать, что M |= ∀x(Xθ), т.е. для всякого объекта a ∈ Dπ верно M |= (Xθ)xa . Предполагая противное, заключаем, что существует такой объект a ∈ Dπ, что формула (Xθ)xa в M ложна. Но тогда M |= ¬(Xθ)xa. Следовательно M |= ∃x¬(Xθ).Но это противоречит предположению M |= ¬∃x¬(Xθ).

Пример 4.2. Покажем, что формула ∀x∃y p(x,y) →∃y∀xp(x,y) не является логическим законом. Для этого необходимо придумать такую модель M, что M |= ∀x∃y p(x,y), но формула ∃y∀xp(x,y) в модели M не является истинной (отметим, что рассматриваемые формулы замкнуты, а потому в любой модели автоматически являются оцененными).

В качестве модели выберем ω — модель элементарной арифметики. Предикатному символу p(x,y) поставим в соответствие отношение x < y на множестве натуральных чисел. Тогда формула ∀x∃y p(x,y) будет означать, что в множестве натуральных чисел с отношением порядка x < y нет максимального элемента, а формула ∃y∀xp(x,y) будет иметь противоположный смысл, что в множестве натуральных чисел есть наибольший элемент. Ясно, что первая формула истинна, а вторая нет.

Две формулы X и Y называются логически эквивалентными, X ≡ Y , если формулаX ~ Y есть логический закон (напомним, что запись X ~ Y — это сокращение формулы (X → Y ) ∧ (Y → X)). Можно сказать иначе: две формулы логически эквивалентны, если в любой модели и при любой оценке они обе или истинны, или ложны.

Теорема 4.2. Если X ≡ Y , то ∀xX ≡∀xY и ∃xX ≡∃xY .

◀ Пусть x, x1, x2, ..., xn — полный набор всех параметров формул X и Y , в котором в качестве первой выбрана переменная x. При произвольно выбранной интепретации языка и при указанном порядке переменных формулы X и Y порождают булевы функции fX(x1,x2,...,xn) и fY (x1,x2,...,xn). Эквивалентность формул означает, что эти функции совпадают. Но тогда

minxfX(x,x1,...,xn) = minxfY (x,x1,...,xn) и

Вычисление минимума или максимума функций fX, fY равносильно навешиванию квантора ∀ или ∃ с переменной x на формулы X, Y . Это указывает на то, что пары формул ∀xX и ∀xY , ∃xX и ∃xY эквивалентны в выбранной модели. Так как модель выбиралась произвольно, заключаем, что эти пары формул логически эквивалентны.▶

Приведем некоторые логические законы. Остановимся лишь на тех, которые выходят за рамки пропозициональных.

Законы де Моргана:

  1. ¬(∀xX) ∼∃x(¬X).
  2. ¬(∃xX) ∼∀x(¬X).

    3. Доказательства общезначимости этих формул аналогичны доказательству общезначимости формулы ¬∃x¬X →∀xX, рассмотренной выше. Одностороннее пронесение кванторов (здесь X не содержит свободно переменной x):

  3. X ∧∀xY (x) ~ ∀x(X ∧Y (x)).
  4. X ∨ ∀ x Y (x) ~ ∀ x (X ∨ Y (x)).
  5. X ∧ ∃ x Y (x) ~∃ x (X ∧ Y (x)).
  6. X ∨ ∃ x Y (x) ~∃ x(X ∨Y (x)).
  7. X →∀ x Y (x) ~ ∀ x (X → Y (x)).
  8. X →∃ x Y (x) ~ ∃ x (X → Y (x)).
  9. ∀ x Y (x)→X ~ ∃ x(Y (x) → X).
  10. ∃ x Y (x)→X ~ ∀ x (Y (x) → X).

    11. Рассмотрим, например, формулу 3. Выберем произвольную модель и в ней произвольную оценку θ. Поскольку x в формулу не входит свободно, считаем, что и в θ переменная x не выходит. Получим оцененную формулу Xθ∧∀xY θ ∼∀x(Xθ∧Y θ), которая является истинной в том и только в том случае, когда обе части эквиваленции имеют одно и то же истинностное значение. Если левая часть импликации истинна, то формулы Xθ и ∀xY θ обе истинны. Значит, при любом a формула (Y θ)xa является истинной. Следовательно, истинна формула Xθ ∧(Y θ)xa . Отсюда вытекает, что формула ∀x(Xθ ∧(Y θ)) в правой части эквиваленции ис-тинна . Нетрудно увидеть, что приведенные рассуждения можно провести в обратном порядке и тем самым показать, что из истинности правой части эвиваленции вытекает истинность левой части.

    Отметим, что доказанная формула 3 имеет естественную интрпретацию при выборе конкретной модели:

    min{fX, minxfY} = minxmin{fX, fY}.


    Это верно при условии , что функция fX не зависит от переменной x.

    Дополнительные законы пронесения кванторов:

  11. ∀xX(x)∧∀xY (x) ~ ∀x(X(x)∧Y (x)).
  12. ∃xX(x)∨∃xY (x) ~ ∃x(X(x)∨Y (x)).
  13. ∃x(X(x)∧Y (x))→∃xX(x)∧∃xY (x).
  14. ∀xX(x)∨∀xY (x)→∀x(X(x)∨Y (x)).

    15. Рассмотрим, например, формулу 11. Выбрав произвольную модель и в ней произвольную оценку θ (считаем, что она не содержит x), получим оцененную формулу ∀xXθ ∧∀xY θ ~ ~∀x(Xθ ∧ Y θ). Истинность левой части означает, что истинны формулы ∀xXθ и ∀xY θ. Следовательно, для любой константы a истинны (Xθ)xa и (Y θ)xa, откуда заключаем, что истинна формула (Xθ)xa ∧(Y θ)xa. Поэтому истинна ∀x(Xθ∧Y θ). Наоборот, если формула ∀x(Xθ∧Y θ)истинна , то для любой константы a истинна формула (Xθ)xa ∧(Y θ)xa . Делаем вывод, что для любой a истинна формула (Xθ)x a и для любой a истинна формула (Y θ)xa . Поэтому истинны формулы ∀xXθ и ∀xY θ, а значит, и формула ∀xXθ∧∀xY θ.

    Логические законы, связанные добавлением кванторов или изменением их порядка:

  15. ∀xX →X.
  16. X →∃xX.
  17. ∃x∃yX ~ ∃y∃xX.
  18. ∀x∀yX ~ ∀y∀xX.
  19. ∃x∀yX →∀y∃xX.

    20. Формулы 15 и 16 можно интерпретировать как утверждение, что для функции u(x) имеет место неравенство

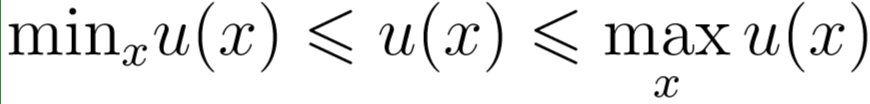
    Формулы 17 и 18 ассоциируются с правилом перестановки максимумов и минимумов по разным переменным, например:

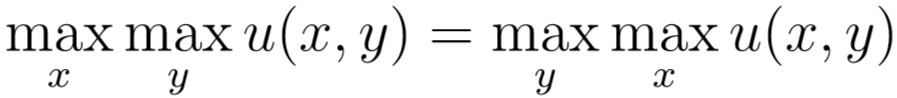
    а формула 19 — отражение неравенства

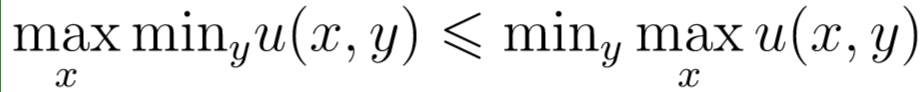
    И в самом деле, u(x,y) ≤ maxx u(x,y). Следовательно, minyu(x,y) ≤ miny maxxu(x,y). В результате справа — константа, а слева — функция переменного x, т.е. miny maxx u(x,y) есть верхняя грань функции minyu(x,y). Значит, имеет место неравенство (4.1).

    Логические законы, связанные с конгруэнтностью (формула X не имеет свободных вхождений переменной y):

  20. ∀xX ~ ∀y Xxy .
  21. ∃xX ~ ∃y Xxy .

Эти логические законы указывают на то, что конгруэнтные формулы логически эквивалентны. Впрочем, эквивалентность конгруэнтных формул лучше доказывать непосредственно, опираясь на индуктивное определение конгруэнтности. Иначе придется доказывать, что конгруэнтная формула получается последовательным переименованием, что интуитивно ясно, но требует формальных рассуждений.

Что касается сформулированных логических законов, то можно рассуждать так (на пример квантора всеобщности). Выбираем произвольную модель и в ней произвольную оценку θ. При этом, поскольку ни x, ни y в формулу ∀xX не входят свободно, можно считать, что и в оценку θ эти переменные не входят. Если переменная x не входит в X свободно, то наличие квантора не играет роли: формула Xθ оказывается оцененной. Если же x входит в X свободно, то формула Xθ будет содержать единственный параметр x. Истинность ∀x(Xθ) означает, что для любого объекта a формула (Xθ)xa оказывается истинной. Но если мы предварительно выполним подстановку (Xθ)xy ), а затем подстановку( ya ), то получим ту же формулу (Xθ)xa ). Она окажется истинной. Аналогичны рассуждения при ложности формулы ∀x(Xθ). Тем самым доказано, что в выбранной модели формулы ∀xX и∀yXxy при любой оценке одновременно истинны или ложны. Значит, они эквивалентны, а формула ∀xX ~ ∀yXxy есть логический закон.