Логико-математические языки

Язык как совокупность четырех множеств (S,C,F,P). Предметные переменные, константы и их сортность. Функциональные и предикатные символы, их тип. Предикатные символы арности 0 как пропозициональные переменные. Индуктивное построение термов и формул. Функциональная сложность терма, логическая сложность формулы. Выражения. Правильные формулы: A(x), B(x,y), C, (∀xA(x)). Комментарии по вариантам построения логико-математических языков. Односортные языки. Свободные и связанные вхождения переменных. Предложения (замкнутые термы и формулы). Соглашения о сокращенной записи формул.

Под логико-математическим языком мы будем понимать совокупность (V, C, F, P) из четырех не более чем счетных множеств, элементы которых называют символами. Первое множество — это множество V предметных переменных. Предметные переменные могут иметь разные сорта. Конкретно мы считаем, что есть еще пятое множество S — множество сортов и задано отображение sort V : V → S. Значение отображения sort V на переменной x ∈ V и есть сорт этой переменной. Каждому сорту π ∈ S соответствует множество Vπ предметных переменных этого сорта, являющееся полным прообразом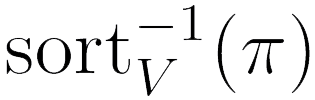 элемента π ∈ S.

Элементы множества C называются константами. Каждая константа относится к определенному сорту π ∈ S, т.е. задано отображение sort_C : C → S множества констант в множество сортов.

Элементы множества F — это функциональные символы, каждый из которых характеризуется своим типом, определяемым кортежем (π₀, π₁, ..., π_n) ∈ Sⁿ⁺¹ сортов (целое число n > 0 называется арностью функционального символа).

Элементы множества P — это предикатные символы, каждый из которых характеризуется своим типом, определяемым кортежем сортов (π₁, ..., π_n) ∈ Sⁿ (и в этом случае n > 0 — арность предикатного символа).

Названия элементов четырех множеств указывают на роль, которые они будут играть в содержательной интерпретации языка. Однако этот содержательный смысл не играет роли в формальной теории. Главное, каким образом из символов составляются правильные слова языка.

В логико-математическом языке два вида правильных слов. Это термы и формулы. Начнем с индуктивного определения термов.

База индукции. Любая переменная или константа сорта π является термом сорта π (элементарные термы).

Шаг индукции. Если t₁, t₂, ..., t_n — термы сортов π₁, ..., π_n соответственно, f — функциональный символ типа (π₀, π₁, ..., π_n), то f(t₁,t₂,,...,t_n) — терм сорта π₀.

Из этого определения нетрудно понять, что термы служат для записи выражений в предметной области (например, многочленов в полях).

Функциональной сложностью терма называется количество функциональных символов в нем. Индуктивно эту характеристику можно определить так: сложность элементарного терма равна 0; сложность терма f(t₁,t₂,...,t_n) равна сумме сложностей аргументов плюс один, т.е.

|f(t1,t2,...,tn)| = |t1|+ t2|+ ... +|tn|+ 1,

где знак модуля обозначает функциональную сложность терма. Подобное индуктивное определение может использоваться не только для определения понятий, но и для доказательства различных утверждений. Например, пусть все элементарные термы обладают свойством P; из того, что термы t₁, t₂, ..., tn обладают свойством P, следует, что терм f(t₁,t₂,...,t_n) также обладает свойством P. Тогда все термы обладают свойством P. Определим теперь формулы. База индукции. Если t₁, t₂, ..., t_n — термы сортов π₁, ..., πn соответственно, p — предикатный символ типа (π₁, ..., π_n), то p(t₁,t₂,...,t_n) — формула (такую формулу будем называть элементарной). Шаг индукции. Если X₁, X₂ — формулы, то (X₁ →X₂), (X₁ ∧X₂), (X₁ ∨X₂), ¬X₁ — формулы. Если X — формула, x — предметная переменная, то ∀xX и ∃xX — формулы. В то время как термы представляют собой записи последовательностей операций над объектами предметной области, формулы обозначают те или иные утверждения о свойствах этих объектов. Совокупность всех термов в рассматриваемом языке обозначим Tm, совокупность всех формул — Fm, а совокупность и тех, и других — Expr. Элементы Expr будем называть выражениями. Отметим, что допускаются предикатные символы арности 0, которые являются элементарными формулами. Множество таких символов в сочетании с логическими связками образует подмножество языка, эквивалентное языку алгебры высказываний. Поэтому предикатные символы арности 0 можно рассматривать как пропозициональные переменные. Для формул может быть введена характеристика, называемая логической сложностью, аналогичная функциональной сложности термов, но определяемая количеством предикатных символов в формуле.

Замечание. 1. На самом деле понятие логико-математического языка можно вводить различными способами, не меняя содержательной сути. Так, предикатные символы можно рассматривать как особый род функциональных символов, для которых сорт π₀ есть " высказывание". Аналогично можно было бы отказаться от переменных языка, рассматривая их как функциональные символы арности 0. В результате дело можно было бы свести к двум множествам: С и F. Отметим также, что множество V на самом деле можно трактовать как семейство множеств, в котором каждое множество — это множество переменных одного сорта. Чтобы обозначить сорт переменной, достаточно указать множество, которому эта переменная принадлежит. Выбор конкретного варианта определения диктуется субъективными факторами, а также тем, что должно присутствовать нечто, трактуемое как сорт высказываний.

2. Совокупность всех переменных, констант, функциональных и предикатных символов плюс логические связки, кванторы, скобки и запятая составляет алфавит логико-математического языка. В данном случае алфавит оказывается счетным множеством. Однако нетрудно дело свести к конечному алфавиту, если считать, что элементы логико-математического языка на самом деле являются словами другого языка (языка нижнего уровня). Так, для всех натуральных чисел можно получить обозначения с помощью двух символов 0 и 1, используя позиционную форму записи. Однако этот механизм находится за пределами интересов математической логики. Поэтому мы и считаем идентификаторы переменных, функций и т.п. простейшими неделимыми элементами языка — символами. #

Среди логико-математических языков выделим односортные языки, в которых все предметные переменные имеют один сорт. Таков язык, например, арифметики. Напротив, язык линейной алгебры является двусортным (числа и векторы).

В формулах ∀xX или ∃xX первый символ называется квантором (далее, если несущественно, какой именно квантор, мы будем использовать обозначение ∇). Комбинация из квантора и переменной называется кванторной приставкой, а формула X, следующая за кванторной приставкой — областью действия квантора. Допускается, что переменная кванторной приставки (кванторная переменная) вообще не имеет вхождений в области действия этой приставки. Появление кванторов приводит к тому, что предметные переменные формулы по своему положению могут иметь разные свойства. В языке высказываний была введена такая операция, как подстановка вместо переменных других переменных или формул. Однако при наличии кванторов произвольная подстановка может привести к неправильной формуле. Например, В формуле ∀x(x > 0) нельзя переменную x заменить произвольной формулой: слово ∀(x + 1)((x + 1) > 0) не является формулой, потому что по индуктивному правилу образования формул сразу за квантором должна следовать переменная, а не служебный символ или константа. Содержательный смысл формулы при такой подстановке также теряется.

Будем говорить, что вхождение предметной переменной x в формулу X является связанным, если оно есть часть кванторной приставки или находится в области действия кванторной приставки с той же переменной. В противном случае вхождение переменной называется свободным. В терме все вхождения каждой переменной свободные.

В одной и той же формуле переменная x может иметь и свободные, и связанные вхождения. Например, в формуле p₁(x,(∀xp₂(x))) три вхождения переменной x, причем первое вхождение свободное, а два других связанные. Если переменная x имеет свободные вхождения в формулу X, то ее называют свободной переменной этой формулы. Отметим, что определенное вхождение переменной может быть связанным в формуле и свободным в некоторой подформуле. Например, предикатный символ, в один из аргументов которого входит переменная, является подформулой, а в элементарной формуле вхождение любой переменной свободное. Еще один пример. В формуле

(∀ xp (x, y) ∧ q (x)) → (∃ x r (x,x))

полужирным шрифтом помечены связанные вхождения переменных, а светлым — свободные.

Свободные переменные, входящие в терм или формулу, называются параметрами этого терма или формулы. Если формула не имеет свободных переменных, то она называется замкнутой или предложением. При записи формул будем использовать сокращения скобок на основе приоритета операций. Наивысшим приоритетом обладают кванторные приставки. Затем идет отрицание, далее дизъюнкция и конъюнкция. Наинизшим приоритетом обладает импликация. Мы будем также использовать сокращение (X ∼ Y ) для формулы ((X → Y ) ∧ (Y → X)), причем символу ~ (эквиваленция) припишем самый низкий приоритет (ниже, чем у импликации). Кроме того, некоторые из функциональных символов арности 2, будем употреблять в инфиксной форме (например, символы алгебраических операций). Все эти соглашения используются для более удобной записи и с теоретическими построениями не связаны. От подобных соглашений всегда можно избавиться, модфицировав соответствующим образом терм или формулу. Разумеется, эти элементы можно было бы включить в формальный язык, но это в теоретическом плане ничего существенного не добавит, хотя заметно усложнит изложение.