Семантика логико-математического языка

Интерпретация логико-математического языка. Предметная область. Интерпретация предметных констант. Интерпретация функциональных и предикатных символов. Интерпретация логических связок и кванторов. Расширение языка введением символов реальных объектов. Оценка и оцененные выражения.

Сами по себе термы и формулы логико-математического языка ничего не значат. Это лишь средство для обозначения или записи реальных объектов. Чтобы термы и формулы приобрели какой-то содержательный смысл, необходимо связать их с реальными объектами из какой-либо области математики, т.е. определить интерпретацию логико-математического языка, или построить модель языка. Для этого мы должны предусмотреть несколько вещей. Во-первых, необходимо придать смысл предметным переменным, определив их возможные значения. Мы назовем носителем (или предметной областью) языка Ω отображение, которое каждому сорту π ∈ S ставит в соответствие некоторое непустое множество D_π. Множество D_π представляет собой носитель сорта π или, другими словами, область изменения переменных сорта π.

Во-вторых, следует придать смысл предметным константам. Естественно каждую константу c ∈ C сорта π связать с некоторым элементомe c˜ ∈ D_πиз носителя сорта π, т.е. задатьотображение e C˜: C → D_π, сохраняющее сортность.

В-третьих, нужно каждому функциональному символу f типа (π₀, ..., π_n) поставить в соответствие конкретное отображение e f˜: D_π1 × ...× D_πn → D_π0, т.е. задать некоторое отображение e F˜: f  → f˜.

В-четвертых, следует каждому предикатному символу p типа (π₁, ..., π_n) поставить в соответствие n-местный предикат того же вида, т.е. отображение, которое каждому элементу множества D_π1 ×...×D_πn ставит в соответствие высказывание. Впрочем, поскольку нас интересует лишь истинность формул, можно ограничиться булевым вариантом и символу p поставить в соответствие отображениеe p: D_π1 ×...×D_πn →B. Отдельно упомянем предикатныесимволы арности 0. Это пропозициональные переменные, которые в случае булевой интерпретации можно заменить двумя булевыми константами.

В-пятых, следует придать смысл всем логическим связкам и кванторам. Мы будем считать, что они имеют общепринятый смысл и что их интерпретация фиксирована. Все сказанное означает, что интерпретация — предписание, которое символам языка ставит в соответствие настоящие объекты. Говорят, что модель языка определяет его семантику. Если задана интерпретация M языка Ω, то каждый терм сорта π определяет отображение, которое каждому набору значений переменных ставит в соответствие объект сорта π, т.е. элемент множества Dπ. Другими словами, терм получает значение, если известны значения всех его параметров. Значение терма легко определить индукцией по построению.

Обычно придание переменным терма некоторых значений рассматривается как некоторый формальный акт подстановки в терм вместо свободных переменных других объектов. Вообще говоря, использовать в выражении конкретные объекты не очень удобно. Во-первых, это выводит за пределы рассматриваемого языка. Во-вторых, подстановка в выражение " неизвестно чего" может привести к неоднозначностям или другим казусам, поскольку так называемые " реальные" объекты вполне могут оказаться словами другого языка.

Указанный формальный подход можно реализовать следующим образом. Введем в обиход дополнительный набор констант, каждая из которых соответствует реальному объекту. Более точно, выберем множество C символов, равномощное D = D_π и биективное отображение , устанавливающее взаимно однозначное соответствие между объектами a ∈ D_π и символами a того же сорта. В формулах будем использовать не сами объекты, о сопоставленные им символы. В результате получим некоторое расширение Ω(D) исходного языка Ω. Теперь мы можем в рамках расширенного языка выполнить формальную подстановку вида

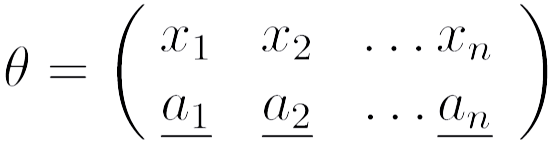
Это константная подстановка, называемая оценкой языка Ω. Если θ содержит все переменные терма T, то терм Tθ оказывается замкнутым выражением (без параметров) и будет иметь конкретное значение. В этом случае θ называется оценкой для выражения T, а само выражение Tθ называется оцененным. В общем оцененное выражение — это любое замкнутое выражение языка Ω(D). Все сказанное переносится и на формулы языка Ω. Значением оцененной формулы является ложь или истина. При этом говорят, что оцененная формула истинна (ложна) в модели M. Подчеркнем, что сами по себе формулы не имеют какого-либо значения. Истинность возникает, когда конкретную интерпретацию получают все функциональные и предикатные символы, а формула не содержит параметров (или все они заменены константами в результате оценки).

Пример 4.1. В качестве примера логико-математического языка рассмотрим язык элементарной арифметики. Этот язык имеет лишь один сорт переменных, которые мы будем обозначать x, y, z, ... Единственную константу обозначим 0. Три функциональных символа f, g, h, из которых первый одноместный, два остальных двуместные. Единственный двуместный предикатный символ обозначим p.

Для функциональных и предикатного символов введем альтернативные бинарные нотации:

f(x) ≡ x+ (переход к следующему натуральному числу);

g(x,y) ≡ (x + y) (операция сложения);

h(x,y) ≡ (x·y) (операция умножения);

p(x,y) ≡ (x = y) (формальное равенство).

Для введенного языка рассмотрим две модели. Первую обозначим ω. Носителем этой модели является множество N₀ целых неотрицательных чисел. Символу 0 поставим в соответствие число нуль. Функциональным символам припишем соответствующие операции над целыми числами. Наконец, равенство (x = y) будет истинным тогда и только тогда, когда два числа x и y совпадают.

Рассмотрим терм (x + y)·z + x⁺. Этому терму мы можем давать различные оценки. Например, при оценке(^{x1 y2 z3} )получим терм (1 + 5)·3 + 1⁺, который в ω имеет значение 20.

Формула ∃y (x+y = z) при оценке(^{x3 z5} )дает истинную оцененную формулу

∃y (3+y = 5). Вто же время при оценке (^{x5 z3} )получим ложную формулу ∃y (5 + y = 3).

Носителем второй модели , которую обозначим R, является множество R действительных чисел. Функциональным символам опять сопоставим сложение, умножение и добавление единицы. Формула x = y выражает совпадение действительных чисел.

Вообще говоря, в качестве интерпретации рассматриваемого языка можно выбрать любое множество D, два любых отображения типа f , g: D² → D, отображение типа h: D → D и отображение p: D →B. Все возможно. Но при этом меняется смысл термов и формул. Например, в модели ω истинна формула x+y = y+x, отражающая арифметический закон. Она сохраняется в модели R, но теряет силу в других моделях.