Предикаты и кванторы
ТеорияОграниченность исчисления высказываний. Переменные высказывания. Cубъект и предикат переменного высказывания. Понятие предиката в математической логике. Арность предиката. Контуры будущей теории. Кванторы как символы агрегирования. Выражения двух видов.
Построенное исчисление высказываний в реальности оказывается довольно бедной теорией. Оно позволяет строить и анализировать различные комбинации высказываний. Однако в математике встречаются предложения, которые, вообще говоря, не являются высказываниями. Например, нельзя сказать, истинно ли утверждение " число x положительное". Ответ зависит от того, какое это число. Здесь мы сталкиваемся с уточнением того, что такое суждение. В каждом суждении присутствуют два компонента — субъект и предикат. Субъект — это понятие, отражающее предмет, о котором идет речь. В предложении субъект связывается с подлежащим. Предикат же можно уподобить сказуемому, поскольку этот структурный элемент выражает свойства, приписываемые предметам или отрицаемые у них. В суждениях " Роза красная", " Гитара семиструнная" субъектами являются " роза" и " гитара", а предикатами — " красная" (все то, что называется красным) и " семиструнная" (все то, что называется семиструнным). В математике этой трактовке суждения отвечает " высказывание с параметрами", т.е. суждение, которое становится высказыванием при конкретизации параметров. Такие суждения называют предикатами. С математической точки зрения предикат можно интерпретировать как некое отображение, которое каждому набору входящих в него параметров ставит в соответствие высказывание. Количество участвующих в предикате параметров называется его арностью.
Понятие предиката не вкладывается в язык исчисления высказываний. Требуется построение более широкой теории, требующей и расширения языка теории. Что должен охватывать такой язык помимо высказываний и логических связок? Во-первых, если в формулах алгебры высказываний встречаются переменные, областью действия которых является множество высказываний, то в формулах любой математической теории есть переменные, область действия которых связана не с высказываниями, а с объектами, изучаемыми в этой теории. В математическом анализе переменные числовые, в геометрии переменные обозначают точки, прямые, плоскости. Такие переменные называют предметными, а область их действия — предметной областью. В теории могут участвовать предметные переменные разного рода, поскольку описывают объекты разных классов (например, точки и прямые в геометрии). Во-вторых, в ряде математических теорий есть установленные символы для обозначения некоторых стандартных объектов (например, число π). В отличие от переменных эти символы имеют конкретное значение. Их называют константами. В третьих, в каждой математической теории используются функции, причем разные, к которым можно отнести и операции над объектами математической теории. Функции можно рассматривать двояко: как отображение и как связь между переменными. С точки зрения формальной записи функция — это символ, который исходя из некоторой совокупности переменных формирует новую переменную (точнее, новый объект, имеющий неопределенное значение). Наконец, в четвертых, в этом языке должны быть отражены и такие символы, как кванторы. Кванторы — специальные символы (или фразеологические штампы), которые позволяют из неопределенного предложения построить правильное высказывание, истинность которого устанавливается однозначно. Кванторы можно рассматривать как символы агрегирования, которые из совокупности возможных значений формируют одно значение. Таковы символы предела, интеграла, суммы. В логике используют два квантора: всеобщности ∀ и существования ∃. Запись ∀xP(x) формирует высказывание, являющееся истинным, если предикат P(x) является истинными для любого возможного значения предметной переменной x. Запись ∃xP(x) формирует высказывание, истинное, если предикат P(x) имеет значение истины хотя бы для одного возможного значения предметной переменной x.
Введение в язык символов агрегирования приводит к тому, что вхождение переменных в формулы может играть две разных роли. В формуле x + y переменным x и y можно присвоить конкретные значения, в результате чего конкретное значение получит все выражение. В формуле ∀xP(x) переменной x нельзя присвоить конкретное значение, поскольку формула подразумевает использование целого множества значений переменной, а не отдельно взятого значения (поэтому и квантор — символ агрегирования). В первом случае говорят о свободном вхождении переменной, а во втором — о связанном вхождении. Одна и та же переменная в выражение может входить и свободно, и связанно. Например, в выражении 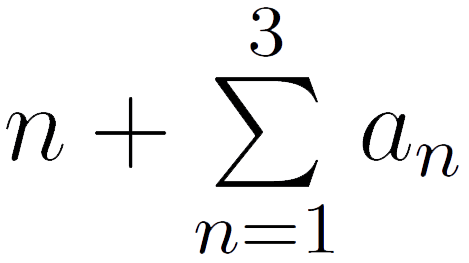 переменная n входит свободно (первое вхождение) и связанно (второе и третье).
переменная n входит свободно (первое вхождение) и связанно (второе и третье).
В дальнейшем изложении мы не будем использовать предметных символов агрегирования, ограничившись только двумя кванторами, так как предметные символы агрегирования усложняют язык, но не добавляют чего-то существенного в формальную теорию как таковую. Отметим, что " за бортом" остаются обозначения множеств и связи множеств и элементов. Если в формальной теории нет средств для обозначения множеств, ее называют теорией 1-го порядка. При введении множеств отдельных элементов получаем теорию 2-го порядка, множества множеств приводят к теории 3-го порядка. И так далее. Отметим, что новая теория будет содержать выражения двух видов. Первые не означают какое-то высказывание, они описывают лишь действия, выполняемые над объектами теории. Например, выражение x+y играет роль новой предметной переменной, значения которой однозначно определяются значениями x и y. Напротив, выражение x + y = 0 выражает суждение, которое может быть истинным или ложным при заданных значениях неизвестных. Разделяя два типа выражений, первые будем называть термами, а вторые формулами. Таким образом, значением терма является некоторый объект теории (например, число), в то время как значением формулы является высказывание.