Глобальные свойства теории N

Выводимые формулы и тавтологии. Непротиворечивость теории N . Полнота теории N . Разрешимость теории N. Независимость аксиом в теории N.

Остановимся на описании множества выводимых формул в теории N. Нетрудно убедиться в том, что все аксиомы этой теории являются тавтологиями . Например, любая аксиома, полученная по схеме 1, может быть получена подстановкой формул в тавтологию x → (y → x), а потому сама является тавтологией (следствие 2.1).

Если формулы X и X → Y являются тавтологиями, то правило modus ponens приводит к формуле Y , также являющейся тавтологией (теорема 2.1). Это означает, что в любом выводе все формулы являются тавтологиями, поскольку либо являются аксиомами, либо получены из тавтологий по правилу modus ponens (аккуратное доказательство может быть проведено методом математической индукции по длине вывода). Можно также утверждать, что если в списке Γ все формулы — тавтологии, то и все формулы, выводимые из гипотез Γ, также будут тавтологиями.

Теорема 3.4. Любая формула, выводимая в теории N, является тавтологией. #

Итак, множество формул, выводимых в теории N содержится в множестве всех тавтологий. На самом деле оба множества совпадают. Чтобы это доказать, установим одно вспомогательное утверждение. Как и в случае булевых функций для произвольной пропозициональной переменной x введем обозначение x^σ, σ ∈ B, полагая, что x¹ = x и x⁰ = ¬x.

Теорема 3.5. Пусть Y — формула, построенная на переменных x₁, ..., x_n, f(ξ₁,...,ξ_n) — истинностная функция формулы Y , α_i∈ B, i = 1, n, — набор истинностных значений для переменных x₁, ..., x_n. Если f(α₁,...,α_n ) = 1, то имеет место выводимость 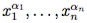⊢ Y. Если f(α₁,...,α_n) = 0,то имеет место выводимость

◀Доказательство строится индукцией по построению формулы. В этом случае базис индукции относится к элементарным формулам, т.е. к переменным. Пусть Y = x и задано истинностное значение α. При α = 1 имеем x^α = x, Y = x, и севенция x^α ⊢ Y истинна, поскольку и левая, иправаячастисеквенции—одна и та же формула. При α = 0 имеем x^α = ¬x,¬Y = ¬x,и истинной является секвенция x^α ⊢ ¬Y .

Чтобы доказать шаг индукции, необходимо в предположении, что утверждение верно для формул Z и W, установить его истинность для формул (Z ∨ W), (Z ∧ W), (Z → W) и (¬Z). Пусть z¹, . . . , zⁿ — общий список переменных формул Z и W .

Рассмотрим случай Y = Z ∧ W . Для заданного набора α значений α¹, . . . , αⁿ введем обозначение 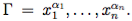Предположим, что на наборе α истинностные функции f_z и f_w принимают значение 1. Тогда по индуктивному предположению имеем Γ ⊢ Z и Γ ⊢ W, откуда по правилу введения конъюнкции получаем выводимость Γ ⊢ Y , так как Y = Z ∧ W . Пусть одна из истинностных функций, например f_Z , принимает значение 0. Тогда имеет место выводимость Γ ⊢ ¬Z. Используя правила естественного вывода, получаем

В результате получена выводимость Γ ⊢ ¬Y , поскольку ¬Y = ¬(Z ∧ W ).

Рассмотрим случай Y = Z ∨ W . Опять выберем набор значений α и введем, как и выше, обозначение Γ. Если одна из функций fZ fW на наборе α имеет значение 1, например fZ^(α) = 1, то по индуктивному предположению имеет место выводимость Γ ⊢ Z. Отсюда сразу получаем выводимость Γ ⊢ Z ∨ W = Y в силу правила введения дизъюнкции. Осталось рассмотреть вариант fZ(α) = fW^(α) = 0. В этом варианте fY ^(α) = fZ^(α) ∨ fW ^(α) = 0 и, значит, нужно установить выводимость Γ ⊢ ¬Y исходя из индуктивных предположений Γ ⊢ ¬Z и Γ ⊢ ¬W.

Имеем:

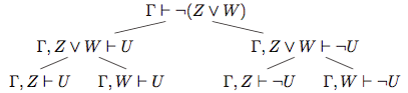
В результате требуемая секвенция оказадась сведена к четырем однотипным севенциям, в которых выбор формулы U (соответственно ¬U) не имеет значения. Истинность всех четырех севенций устанавливается по единому сценарию с помощью закона противоречия. Рассмотрим, например, первую из них:

Рассмотрим случай Y = Z → W . Выделим вариант fW ^(α) = 1. В этом варианте fY ^(α) = 1 и нужно установить выводимость Γ ⊢ Z → W исходя из Γ ⊢ W. Это верно в силу правила присоединения посылки. Пусть fZ (α) = 1, fW ^(α) = 0. Тогда fY ^(α) = 0, и нужно установить выводимость Γ ⊢ ¬(Z → W) исходя из Γ ⊢ Z и Γ ⊢ ¬W. Это можно сделать следующим образом:

Пусть fZ^(α) = 0, fW ^(α) = 0. Тогда fY (α) = 1, и требуется установить Γ ⊢ Z → W исходя из Γ ⊢ ¬Z и Γ ⊢ ¬W. Из первой секвенции добавлением гипотезы получаем Γ,Z ⊢ ¬Z, что с очевидной секвенцией Γ, Z ⊢ Z по закону противоречия приводит к выводимости Γ, Z ⊢ W и далее по правилу введения импликации к Γ ⊢ Z → W .

Рассмотрим случай Y = ¬Z. Если fZ^(α) = 1, то fY ^(α) = 0 и Γ ⊢ Z. Введением отрицания получаем Γ⊢¬¬Z = ¬Y. Аналогично при fZ^(α) = 0 имеем fY^(α) = 1 и Γ⊢¬Z, что равносильно Γ ⊢ Y . ▶

Теорема 3.6. Любая тавтология Y выводима в теории N.

◀Пусть формула Y построена из переменных x₁, . . . , x_n. Поскольку Y — тавтология, ее истинностная функция на любом булевом векторе α принимает значение 1. Значит, для любых значений α₁,...,α_n имеет место выводимость

Обозначим 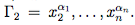Имеют место выводимости x₁ ,Γ₂ ⊢ Y и ¬x₁ ,Γ₂ ⊢ Y. Поправилу удаления конъюнкции находим x₁ ∨ ¬x₁, Γ₂ ⊢ Y . Используя выводимость ⊢ x₁ ∨ ¬x₁, по правилу сечения получаем Γ₂ ⊢ Y .

Повторяя рассуждения, последовательно убираем из списка гипотез переменные x₂, x₃ и т.д. В конечном счете получим выводимость ⊢ Y , что равносильно утверждению теоремы. ▶

Полученное описание выводимых в теории N формул позволяет установить такие свойства этой теории, как непротиворечивость, полноту и разрешимость. Установление этих свойств — цель, преследуемая при формализации любой теории.

Под непротиворечивостью формальной теории понимают отсутствие в этой теории такой формулы X, для которой выводимыми являются и сама формула X, и ее отрицание ¬X. Ино- гда дают такое определение непротиворечивости теории: теория непротиворечива, если в ней существует невыводимая формула. Формально утверждение о выводимости любой формулы сильнее, чем утверждение о выводимости какой либо пары X и ¬X (из первого утверждения очевидно вытекает второе). Однако в данном случае оба подхода дают одно и то же: если в теории выводимы и X, и ¬X, то по закону противоречия выводима любая формула.

Теорема 3.7. Теория N является непротиворечивой.

◀Выводимыми в теории N являются только тавтологии. Если формула X выводима в теории N, то X — тавтология. Но тогда ¬X является противоречием и не относится к числу выводимых формул. ▶

Под полнотой формальной теории понимают свойство, согласно которому не существует такой невыводимой формулы X, добавление которой к аксиомам приводит к непротиворечивой теории. Другими словами, в такой теории Для каждой формулы X выводима либо сама фор- мула, либо ее отрицание. Наша теория не полна в этом смысле. Действительно, если, добавив в качестве аксиомы некоторую формулу X, мы найдем вывод формулы ¬X, то, с иной точки зрения, мы получим вывод ¬X из гипотезы X в теории N, т.е. X ⊢ ¬X. Значит, согласно де- реву (3.1), имеет место выводимость ⊢ ¬X. Однако, как доказано, такое возможно только, если X — противоречие. Следовательно, добавление любой формулы, не являющейся тавтологией или противоречием, дает непротиворечивую теорию.

Впрочем, если в теорию ввести дополнительную схему аксиом, построенную на формуле, не являющейся тавтологией, то подставляя в схему вместо символов подстановки определенные формулы, можно получить противоречие. Это противоречие, с одной стороны, является аксио- мой, поскольку получено из схемы аксиом, а с другой стороны, его отрицание есть тавтология, выводимая в теории N. Пусть например, схема аксиом построена на формуле, представленной истинностной функцией f(x₁, . . . , x_n). Так как формула — не тавтология, существует набор значений α₁, . . . , α_n аргументов функции, на котором она принимает значение 0. Каждую переменную xj заменим формулой x_j ∨ ¬x_j, если α_j = 1, и формулой x_j ∧ ¬x_j. Полученная формула, построенная по схеме аксиом, будет противоречием.

При построении исчисления высказываний (и далее исчисления предикатов) различают полноту в широком смысле, означающую сказанным выше, и полноту в узком смысле, означающую, что выводимыми являются все тавтологии. В узком смысле теория N полна. Впрочем, отсутствие полноты в широком смысле легко устраняется простой модификацией формальной теории: достаточно вместо каждой схемы аксиом записать обычную аксиому, заменив места подстановки переменными и добавить еще одно правило вывода, заключающееся в подстановке вместо переменных произвольных формул. Отметим, что свойством полноты обладают очень простые математические теории: согласно теореме Геделя о неполноте любая достаточно со- держательная теория не является полной, поскольку в рамках такой теории удается построить такую формулу Z, что ни эта формула, ни ее отрицание не являются выводимыми.

Под разрешимостью теории понимают наличие алгоритма, который для любой формулы позволяет установить за конечное число элементарных операций, выводима эта формула или нет. В данном случае в качестве такого алгоритма может рассматривать процедуру построения истинностной функции и проверки ее на наличие значений 0. Отсутствие таких значений означает, что функция является постоянной, а формула — тавтологией, т.е. выводимой в теории N. Указанная процедура выполняется за конечное число алгебраических операций и дает однозначный ответ, выводима формула или нет. В этом смысле теория N является разрешимой теорией.

Еще один вопрос, связанный с построением формальной теории — независимость аксиом. Аксиома формальной теории не зависит от остальных аксиом этой теории, если эта аксиома не является выводимой формулой в теории, которая получается из исходной удалением указан- ной аксиомы. Если ни одна из аксиом формальной теории не является логическим следствием остальных, то говорят о независимой системе аксиом.

Система аксиом теории N является независимой в том смысле, что удалив одну из схем аксиом теории, мы не сможем вывести ни одну из формул, получаемой в рамках этой схемы аксиом. Как можно доказать утверждения подобного рода. Напомним, что в формальной теории формулы теряют всякий содержательный смысл; например, знак импликации может озна- чать какую угодно бинарную операцию на множестве возможных значений переменных, а сами переменные могут быть связаны с любыми математическими объектами. Придание смысла символам формальной теории называют интерпретацией этой теории. В данном случае множество всех высказываний, как область изменения переменных и естественный логический смысл символов операций — это одна из возможных интерпретаций исчисления N.

Интерпретация формальной теории строится в рамках какой-либо другой математической теории. Надежность интепретации определяется надежностью той теории, в которой интепретируется исчисление. Так, суждения о непротиворечивости, полноте и разрешимости исчисления N получены в рамках так называемой теории булевых функций, т.е. теории функций с областью изменения переменных и функций 0 и 1. В этом смысле подобные суждения носят относительный характер. В математике считают абсолютно надежными теории, связанные с конечными множествами. В этом смысле утверждения о непротиворечивости, полноте и разрешимости исчисления N являются абсолютными. Утверждение о независимости системы аксиом тоже будет абсолютным, если оно будет получено на базе какой-либо конечной интерпретации.

Теорема 3.8. Схемы аксиом исчисления N не зависят друг от друга.

◀Наиболее просто доказать независимость схем, начиная с 3-й, так как все эти схемы исполь- зуют, кроме импликации, еще одну операцию, которая участвует лишь в двух других схемах аксиом. Можно ограничиться двухэлементной областью изменения переменных и стандартной интепретацией операций, кроме одной. В табл. 3.1 приведены схемы аксиом и новая интер- претация одной из операций. При этой интерпретации указанная схема аксиом при некоторых значениях входящих в нее формул принимает значение 0, в то время как остальные аксиомы имеют постоянное истинностное значение 1. Изменение интерпретации не затрагивает правила modus ponens, так что при удалении указанной схемы аксиом мы получаем теорию, в кото- рой все выводимые формулы — тавтологии, но некоторые формулы, получаемые из указанной схемы, выводимыми не являются. Это и означает, что указанная схема аксиом не зависит от остальных.

Независимость первых двух схем доказать сложнее, поскольку они касаются импликации, затрагивающей все схемы. Ответ можно найти, рассмотрев в качестве области изменения переменных множество из трех целых чисел {0, 1, 2} и выбрав следующие интерпретации операций: x ∧y = min{x, y}, x∨y = max{x, y}, ¬x = 2−x. Для импликации потребуем выполнения условия, что x → y = n тогда и только тогда, когда x ≤ y. При поставленных условиях схемы 3, 4, 6, 7, 10, 11 будут давать формулы с тождественным значением n, а в силу условия, наложенного на импликацию, значение Y будет тождественное n при X ≡ n и X → Y ≡ n. Недоопреде- ленность импликации можно использовать для получения нужных значений первых двух схем аксиом и для обеспечения тождественного значения n схем 5, 8, 9.

Положим x → y = 0 при x > y. Тогда схема X → (Y → X) будет иметь значение 0 при X = 1, Y = 2, в то время как остальные аксиомы будут давать тождественное значение 2. Действительно, в схеме 2 исключаем случай X > Y или X ≤ Z, так как тогда она имеет вид 0 → W илиW → 1. Значит,Z < X ≤ Y и схема имеет вид 2 → (X → 0 → 0). Но X > Z ≤ 0,значит, X → 0 = 0 и 2 → (X → 0 → 0) = 2 → (0 → 0) = 2 → 2 = 2. В схеме 5 исключаем случаи ̆X > Y или X > Z, когда она имеет значение 2. Но тогда X ≤ min{Y, Z} и X → Y ∨ Z = 2. Поэтому X → Y → (X → Z → (X → Y ∧ Z)) = X → Y → (X → Z → 2) = 2. В схеме 8 исключаем случай X > Z или Y > Z. Тогда max{X,Y} ≤ Z,X∨Y → Z = 2 и схема 8 имеет тождественное значение 2. В схеме 9 исключаем случай X > Y. Но тогда X ≤ Y, ¬Y ≤ ¬X и формула имеет вид 2 → 2.

Положим x → y = 1 при x > y. Тогда схема 8 будет иметь значение 1, например, при X = 1, Y = 2, Z = 0. В схеме 1 исключаем случай̆ Y ≤ X. Тогда X < Y ≤ 2, а значит, X ≤ 1и X → (Y → X) = X → 1 = 2. Схемы 5, 8, 9 проверяются так же, как выше. ▶

Таблица 3.1