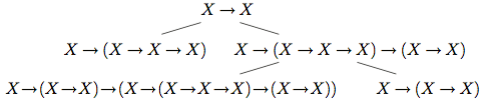Основные положения теории N
ТеорияЯзык теории N. Аксиомы (их одиннадцать): 1) X → (Y → X); 2) X → Язык теории N. Аксиомы (их одиннадцать): 1) X → (Y → X); 2) X → Y → (X → (Y → Z) → (X → Z)); 3) X∧Y → X; 4) X∧Y → Y; 5) (X → Y) → ((X → Z) → (X → Y ∧Z)); 6) X → X∨Y; 7)Y → X∨Y;8)X → Z → (Y → Z → (X∨Y → Z));9)X → Y → (¬Y → ¬X);10)¬¬X → X; 11) X → ¬¬X. Правило вывода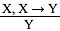 
(modus ponens). Вывод в теории N. Вывод из Y гипотез. Пример: X → X. Дерево вывода. Язык теории N — э
то язык алгебры высказываний. В теории N одиннадцать схем аксиом. Схема аксиом отличается от аксиомы тем, что в ней используются не конкретные пе- ременные, а символы подстановки, вместо которых могут подставляться конкретные формулы теории. При выборе вместо символов подстановки конкретных формул мы получаем конкрет- ную аксиому. Отметим, что можно было бы избежать схем аксиом,о тогда придется вводить дополнительные правила вывода, которые позволили бы ”размножить“ аксиому.
Язык теории N — это язык алгебры высказываний. В теории N одиннадцать схем ак- сиом. Схема аксиом отличается от аксиомы тем, что в ней используются не конкретные переменные, а символы подстановки, вместо которых могут подставляться конкретные формулы теории. При выборе вместо символов подстановки конкретных формул мы получаем конкретную аксиому. Отметим, что можно было бы избежать схем аксиом, но тогда придется вводить дополнительные правила вывода, которые позволили бы ”размножить“ аксиому.
Итак, сформулируем одиннадцать схем аксиом теории N:
1) X → (Y → X); |
7) Y → X ∨ Y ; |
В теории N всего одно правило вывода — правило заключения (modus ponens):
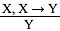
Представленная запись означает, что из двух ”правильных“ формул вида X и X → Y вытекает ”правильная“ формула Y .
После введения языка, аксиом и правил вывода формальная теория готова. Дальше можно начинать ”игру в слова“ и получать теоремы (т.е. выводимые формулы) этой теории. На этом, собственно, заканчивается формальная часть и начинается неформальная, т.е. метатеория. Основной вопрос: что дает формальная теория в качестве выводимых формул. Отметим, что добросовестный вывод даже простых теорем оказывается весьма трудоемким, и следует прибегать к приему, хорошо известному математикам: использовать уже выведенные теоремы наравне с аксиомами.
Выводом теории N будем называть последовательность формул X1, X2, . . . , Xn, в которой каждая формула Xi есть либо аксиома, либо получена из каких-либо предшествующих формул Xk, Xm (k, m < i) по правилу modus ponens. Формула X называется выводимой в теории N, если она является конечной формулой некоторого вывода. Этот факт будем обозначать следующим образом: ⊢ X.
Для нас будет важен условный вывод, или выод из гипотез, при котором некоторые формулы мы предполагаем истинными и на основании этого строим вывод. Такой условный вывод играет промежуточную роль, позволяя рассматривать отдельные части окончательного вывода. Кроме того, условный вывод можно рассматривать как построение вывода из нелогических ак- сиом, которые присутствуют во всех математических теориях (они характеризуют основные положения теории). Далее большими греческими буквами будем обозначать списки формул теории N.
Выводом из гипотез Γ в теории N будем называть последовательность формул, в ко- торой каждая формула есть либо аксиома, либо формула из списка Γ, либо она получена из предшествующих формул по правилу modus ponens. При этом конечная формула X любого вывода из гипотез Γ называется выводимой из гипотез Γ, что обозначается следующим образом: Γ ⊢ X.
Пример 3.1. Построим вывод формулы X → X, где X — какая-либо формула теории N:
- из схемы 1 получаем аксиому X → (X → X);
- из схемы 2, заменяя Z на X и Y на X → X, получаем аксиому X → (X → X) → (X → (X → X → X) → (X → X)),
- из двух предыдущих формул по правилу вывода X → (X → X → X) → (X → X);
- из схемы 1 при X → X взамен Y получаем аксиому X → (X → X → X);
- из двух последних формул по правилу вывода X → X.
