Правила естественного вывода

^Теория

Теорема о дедукции: если Γ, X ⊢ Y , то Γ ⊢ X → Y . Структурные правила естественного вывода. Логические правила естественного вывода. Дополнительные правила естественного вывода: присоединение посылки; закон противоречия; двойное отрицание; доказательство от противного; удаление конъюнкции справа. Обобщенное правило введения дизъюнкции.

Одна из целей введения исчисления высказываний — анализ используемой практики построения доказательств. В качестве единственного правила вывода в теории взято правило modus ponens, в то время как построение доказательств на практике использует и многие другие правила: правило исключенного третьего, доказательство от противного и т.п. Оказывается, что все подобные правила можно получить из аксиом исчисления высказываний и правила modus ponens.

Веденный символ ⊢ выводимости в исчислении высказываний позволяет строить формулы нового типа Γ ⊢ X, которые на содержательном уровне можно интерпретировать так: ”если истинны формулы списка Γ, то истинна формула X. Это формулы метаязыка, позволяющие упростить процесс установления того, выводима данная формула или нет. Само правило modus ponens можно трактовать как формулу X, X → Y ⊢ Y . Формулу вида Γ ⊢ X будем называть секвенцией. Секвенция — это логическая формула, которая может быть истинной или нет.

Чтобы приблизиться к общепринятой практике доказательств, выведем в теории N ряд дополнительных правил, называемых правилами естественного вывода. Следующая теорема дает основополагающее правило естественного вывода, в некотором смысле обращающее правило modus ponens. Фактически эта теорема представляет собой утверждение об эквива- лентности символа импликации → и символа выводимости ⊢.

Теорема 3.1 (теорема о дедукции). Если Γ, X ⊢ Y , то Γ ⊢ X → Y .

◀ Доказательство строится на анализе последовательности вывода. Фактически надо показать, что для любого вывода Z₁, Z₂, . . . , Z_n = Y из гипотез Γ, X существует вывод из гипотез Γ формулы X → Y . Доказательство проведем индукцией по длине вывода.

При n = 1 конечная формула вывода Zn = Y есть либо аксиома, либо формула из списка Γ, либо формула X (правило modus ponens в данном случае не применялось, так как длина вывода меньше двух). В первом и втором случаях строим последовательность формул Y , Y → (X → Y ) (аксиома схемы 1), X → Y (modus ponens), которая является выводом формулы X и списка гипотез Γ. В третьем случае X = Y и формула X → Y совпадает с выводимой формулой X → X (см. пример 3.1). Таким образом, при n = 1 утверждение доказано.

Предположим, что утверждение доказано для всех формул Y , имеющих вывод из гипотез Γ, X длины менее n. Рассмотрим произвольный вывод Z₁, Z₂, . . . , Z_n = Y . Формула Y есть либо аксиома, либо формула из списка Γ, либо X, либо получена по правилу modus ponens. В первых трех случаях рассуждения те же, что и при n = 1 (в выводе можно оставить только последнюю формулу и свести дело к n = 1). Рассмотрим случай, когда Y получена по правилу modus ponens из формул Z_k и Z_j. В этом случае одна из формул, например Z_j, есть импликация Z_k → Y . В соответствии с индукционным предположением из гипотез Γ выводимы формулы X → Z_k и X → (Z_k → Y ). Объединим два этих вывода, удалив из списка повторения формул, если они есть*. Дополняем полученное объединение следующими тремя формулами:

X → Zk → (X → (Zk → Y) → (X → Y)) (аксиомасхемы2);

X → (Zk → Y) → (X → Y)(modusponens);

X → Y (modus ponens).

В результате получаем вывод формулы X → Y из гипотез Γ. В соответствии с методом математической индукции утверждение теоремы доказано для конечной формулы любого вывода из гипотез Γ, X. ▶

Следующая теорема устанавливает пять правил, называемых структурными правилами естественного вывода. Правила сформулированы не для формул языка алгебры высказываний, а для секвенций. Они позволяют из уже известных выводимостей получать новые. При этом соответствующий вывод на самом деле не строится, а лишь формулируется заключение о существовании такого вывода.

Теорема 3.2. Для любых списков формул Γ и ∆ и любых формул X, Y , Z истинны следующие секвенции:

Γ, X, ∆ ⊢ X (закон тождества);
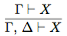(правило добавления гипотез);
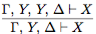(правило сокращения гипотез);
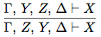(правило перестановки гипотез);
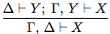(правилосечения).

Правила, обозначенные в теореме, — элементарные следствия из определения понятия ”вывод из гипотез“ и лишь фиксируют очевидное.

Отметим также очевидный факт, что мы можем произвольно вводить аксиомы в список Γ гипотез или выводить аксиомы из списка, не меняя сути. Первое вытекает из правила добавления гипотез, а второе утверждение можно получить как формальное следствие правила сечения:

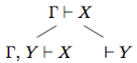
Следующая теорема вводит так называемые логические правила естественного вывода, описывающие некоторые общепринятые приемы проведения математических доказательств.

Теорема 3.3. Для любого списка формул Γ и любых формул X, Y , Z верны следующие утверждения:

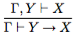(введение импликации, теорема о дедукции);
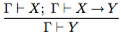(удаление импликации, modus ponens);
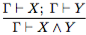(введение конъюнкции);
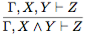(удаление конъюнкции);
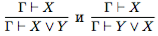(введение дизъюнкции);
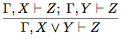(удаление конъюнкции, правило разбора случаев);
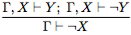(введение отрицания);
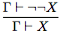)(удаление отрицания).

◀Первые два правила — это теорема о дедукции и правило modus ponens в применении к выводу из гипотез. В самом деле, объединив выводы из Γ формул X и X → Y , получим последовательность, в которой есть эти формулы. Применив modus ponens, получим Y , которую добавим в конец последовательности формул. Получим вывод Y из Γ.

Для доказательства правила 3 для произвольно заданных формул X и Y используем какую- либо аксиому T и аксиому T → X → (T → Y → (T → X ∧Y )) схемы 5. Из выводимости формул X и Y из списка Γ следует выводимость формул T → X и T → Y . Дважды удаляя импликацию в аксиоме схемы 5, получим выводимость T → X ∧ Y . Еще раз удаляя импликацию (T выводима), получаем выводимость X ∧ Y . Указанную последовательность шагов можно представить в виде дерева

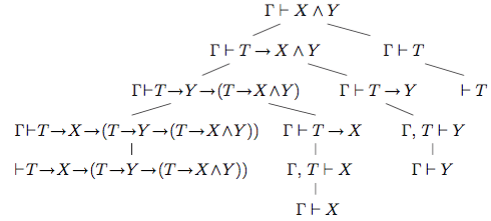
Правило 4 опирается на аксиомы X ∧Y → X и X ∧Y → Y. Из этих аксиом по правилу modus ponens получаем выводимости X ∧ Y ⊢ X и X ∧ Y ⊢ Y . Остается соединить два этих вывода с выводом Γ, X, Y ⊢ Z для получения нужного вывода Γ, X ∧ Y ⊢ Z. Соответствующее дерево вывода имеет следующий вид:

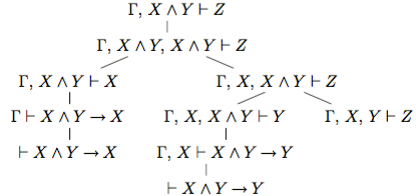
(здесь использовано упрощенное правило 2 вида. 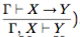Аналогично доказывается правило Γ, X ⊢ Y 5, но с использованием аксиом X → X ∨Y и X → Y ∨X, полученных по схемам 6 и 7.

Правило 6 опирается на аксиому X → Z → (Y → Z → (X ∨Y → Z)), полученную по схеме 8 и выводится аналогично правилу 5:

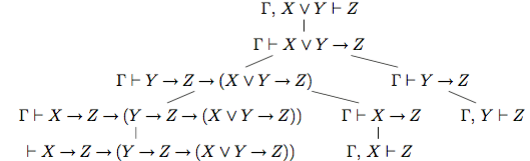
Правило 8 опирается на схему аксиом 10 и доказывается следующим деревом:

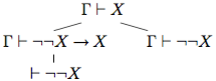
Отметим, что из схемы 11 вытекает правило, обратное к правилу 8: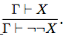

Остановимся на правиле 7, которое вытекает из схем 9, 10, 11. Непосредственно из схемы аксиом 9 вытекает более слабое правило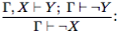

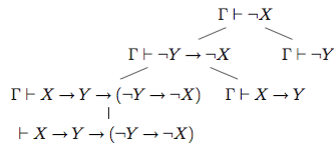
Чтобы получить нужное правило, необходимо в список Γ добавить аксиому X. Получим правило,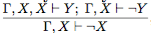 или после сокращения одинаковых гипотез: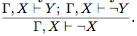Остается обосновать правило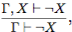для чего используется схема аксиом 11. Кроме того, как и вслучае правила 5 используется какая-либо аксиома T . Эта аксиома вводится в список гипотез,а затем дважды применяется слабый вариант доказываемого правила (3.1):

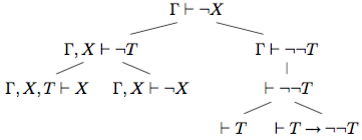
Теорема полностью доказана.▶

Как видно по комментариям в формулировке теоремы, логические правила естественного вывода есть двух видов: правила введения, которые позволяют доказывать формулу с данной логической связкой, и правила удаления, которые показывают, как использовать эту формулу для доказательства других формул.

Правила естественного вывода (в первую очередь, теорема о дедукции) позволяют устанавливать выводимость в исчислении высказываний тех или иных формул, не строя конкретного вывода. Достаточно опираться на установленные правила и, как показано, в доказательстве теоремы, строить вывод, но уже других формул — секвенций. Отметим, что набор правил естественного вывода самодостаточен: в этих правилах учтены все схемы аксиом. При установлении истинности секвенций нет нужды прибегать непосредственно к аксиомам. Как станет ясно из дальнейшего изложения, выводимость формулы X равносильна тому, что секвенция ⊢ X выводима из правил естественного вывода.

На практике при установлении истинности конкретных секвенций удобно использовать дополнительные правила, вытекающие из правил естественного вывода. Укажем некоторые простейшие следствия правил естественного вывода.

Пример 3.2. а. Правило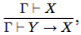 называемое присоединением посылки, вытекает из Γ⊢Y → X правила введения импликации и правила добавления гипотез:

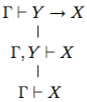
б. Правило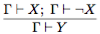(закон противоречия) вытекает из правила введения отрицания добавлением гипотез:

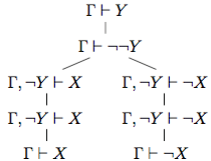
в. Правило введения двойного отрицания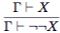может быть получено из схемы аксиом 11. Его можно также вывести из правил естественного вывода:

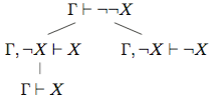
г. Полезно правило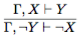доказательства от противного, которого вытекает из правила введения отрицания:

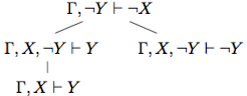
д. Правила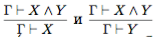удаления конъюнкции справа вытекают из правила удале- Γ⊢X Γ⊢Y ния конъюнкции (но также могут быть получены из схем аксиом 6 и 7). Например, первое из этих правил получается применением правила сечения и правила удаления конъюнкции:

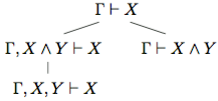
Второе правило удаления конъюнкции справа можно получить аналогично. #

Правила естественного вывода и их следствия позволяют доказать выводимость широкого круга секвенций. Однако отметим, что наиболее тяжело устанавливаются выводимости вида Γ ⊢ X ∨ Y . Правило введения дизъюнкции сводит задачу к выводу более сильного утверждения Γ ⊢ X или Γ ⊢ Y .

Пример 3.3. На практике для доказательства утверждения вида X ∨ Y можно рассуждать так: ”пусть X не верно, т.е. истинно ¬X. Докажем, что тогда истинно Y .“ Этому варианту рассуждений соответствуют правила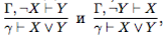которые можно получить и в ис- γ⊢X∨Y γ⊢X∨Y числении высказываний. Для этого достаточно использовать правило введения отрицания и правило доказательства от противного:

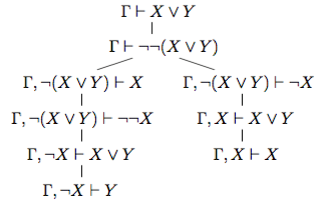
Это правило назовем обобщенным правилом введения дизъюнкции.