Минимизация ДНФ
ТеорияМинимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.
Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.
Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.
В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.
Отдельные элементы, составляющие булев куб Bn, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i1, ..., ik, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.
Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x1 = 0, x4 = 0, x4 = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).
Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bn. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.
Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.
Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.
Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная xi. Это позволяет не различать булевы функции и формулы, составленные из переменных x1, . . . , xn. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.
Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть di и ni, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.
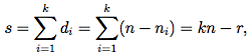
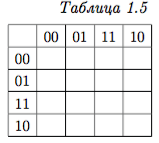 |
При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5). |
В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.
На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.
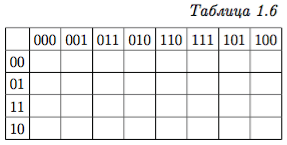 |
К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных. |
Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).
Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.
 |
Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3. |
Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.
Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x2x4+x1x2x4+x1x2x3x4+x1x2x3x4 нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.
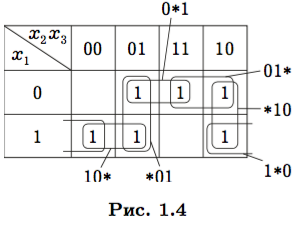 |
Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить. |
Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-
канты 1∗0, ∗01, 01∗.Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.
Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.
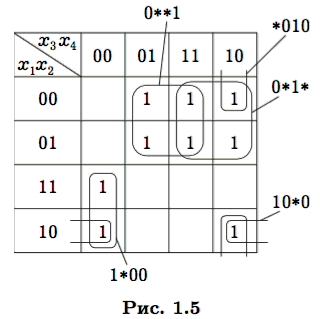 |
Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. # |
Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK1 +xK2 заменяется суммой xK1 +xK2 +K1K1. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K1K2. После завершения первого этапа выполняется операция поглощения согласно формуле K1K2 + K2 = K2.
Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K1, K2, . . . , Km. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками Ki1 , Ki2 , . . . , Kip . Тогда элементарная дизъюнкция Ki1 + Ki2 + . . . + Kip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.
Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.
Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:
Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:
Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим
Используя дистрибутивность и идемпотентность, приходим к ДНФ:
Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K1, K2, K3, K4 и K1, K2, K3, K5. В результате получим
Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K4 + K5. Добавив к каждому слагаемому элементарную конъюнкцию K1K2K3, описывающую ядро, получим полную функцию Патрика. #
Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содержится хотя бы одна выделенная единица, все простые импликанты ядровые, т.е. рассматриваемая функция имеет единственную тупиковую ДНФ.
Минимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.
Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.
Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.
В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.
Отдельные элементы, составляющие булев куб Bn, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i1, ..., ik, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.
Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x1 = 0, x4 = 0, x4 = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).
Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bn. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.
Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.
Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.
Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная xi. Это позволяет не различать булевы функции и формулы, составленные из переменных x1, . . . , xn. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.
Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть di и ni, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.
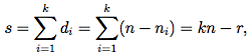
 |
При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5). |
В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.
На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.
 |
К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных. |
Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).
Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.
 |
Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3. |
Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.
Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x2x4+x1x2x4+x1x2x3x4+x1x2x3x4 нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.
 |
Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить. |
Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-
канты 1∗0, ∗01, 01∗.Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.
Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.
 |
Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. # |
Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK1 +xK2 заменяется суммой xK1 +xK2 +K1K1. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K1K2. После завершения первого этапа выполняется операция поглощения согласно формуле K1K2 + K2 = K2.
Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K1, K2, . . . , Km. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками Ki1 , Ki2 , . . . , Kip . Тогда элементарная дизъюнкция Ki1 + Ki2 + . . . + Kip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.
Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.
Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:
Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:
Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим
Используя дистрибутивность и идемпотентность, приходим к ДНФ:
Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K1, K2, K3, K4 и K1, K2, K3, K5. В результате получим
Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K4 + K5. Добавив к каждому слагаемому элементарную конъюнкцию K1K2K3, описывающую ядро, получим полную функцию Патрика. #
Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содер