ДНФ и КНФ

Стандартный базис. Элементарные формулы — литералы. Элементарная конъюнкция (дизъюнкция). Дизъюнктивная (конъюнктивная) нормальная форма и совершенная форма. Теорема: любая булева функция, отличная от 0 (от 1) представима в виде СДНФ (СКНФ). Полнота стандартного базиса. Примеры полных базисов: базис Жегалкина, штрих Шеффера, стрелка Пирса.

Стандартный базис — это набор из трех исходных операций булевой алгебры: сложения (объединения), умножения (пересечения) и отрицания.

Здесь мы будем называть литералом переменную x или ее отрицание x и обозначать xˆ. Булево пересечение нескольких литералов, определяемых различными переменными, т.е. выражение вида X = xˆ₁xˆ₂ . . . xˆ_л, называется элементарной конъюнкцией. Требование, чтобы все переменные были различны обусловливается следующим. Если в конъюнкцию входит несколько одинаковых литералов, то в силу коммутативности, ассоциативности и идемпотентности конъюнкции можно, переходя к эквивалентной формуле, оставить лишь один литерал (например, x₁x₁ = x₁). Если в конъюнкцию входит переменная и ее отрицание, то формула эквивалентна константе 0, поскольку x x = 0 и для любой формулы Y имеем Y x x = 0.

Дизъюнкция нескольких элементарных конъюнкций называется дизъюнктивной нормальной формой, или ДНФ. Например,

x₁ x₃ + x₂ x₃x₄ + x₁ x₂ x₃ x₅.

Если состав переменных в каждой элементарной конъюнкции данной ДНФ один и тот же, то ДНФ называется совершенной. Приведенный пример — это ДНФ, не являющаяся совершен- ной. Напротив, формула

x₁x₂x₃x₄ +x₁x₂x₃x₄ +x₁x₂x₃x₄

есть совершенная форма.

Поскольку в булевой алгебре сложение и умножение — симметричные операции и всегда можно интерпретировать сложение как умножение, а умножение как сложение, существует и двойственное понятие — конъюнктивная нормальная форма (КНФ), представляющая собой конъюнкцию элементарных дизъюнкций, и совершенная конъюнктивная форма (СКНФ). Из принципа двойственности для симметричных полуколец вытекает, что любому утверждению относительно ДНФ отвечает двойственное утверждение относительно КНФ, которое получается заменой сложения (дизъюнкции) умножением, умножения (конъюнкции) сложением, константы 0 константой 1, константы 1 константой 0, отношения порядка двойственным (обратным) порядком. Поэтому далее мы остановимся на изучении только ДНФ.

Теорема 1.4. Любая булева функция, отличная от константы 0 представима в виде СДНФ.

◀Условимся под x^σ понимать формулу x, если σ = 1, и формулу x, если σ = 0. Пусть функция f(y₁, . . . , y_n) принимает значение 1 на векторе (t₁, . . . , t_n) (такой вектор называют конституэнтой единицы). Тогда элементарная конъюнкция 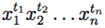также принимает значение 1 на этом наборе, но обращается в нуль на всех остальных n-мерных булевых векторах. Рассмотрим формулу

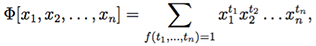
в которой сумма (объединение) распространяется на все те наборы (t₁, . . . , t_n) значений аргументов, на которых заданная функция принимает значение 1. Отметим, что множество таких наборов не пусто, так что в сумме есть по крайней мере одно слагаемое.

Нетрудно заметить, что формула Φ обращается в 1 при тех, и только при тех значениях переменных, при которых обращается в 1 рассматриваемая функция. Значит, формула Ψ представляет функцию f. ▶

Следствие 1.1. Стандартный базис является полным.

◀ Действительно, если функция не является константой 0, то она представима либо в виде СДНФ, которая является формулой над стандартным базисом. Константу 0 можно представить, например, формулой f(x₁, x₂, . . . , x_n) = x₁x₁. ▶

Пример 1.2. Рассмотрим функцию трех переменных m(x₁, x₂, x₃) (табл. 1.4), называемую мажоритарной функцией. Эта функция принимает значение 1, если больше половины ее аргументов имеют значение 1. Поэтому ее часто называют функцией голосования. Построим для нее СДНФ.

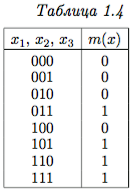Мажоритарная функция имеет 4 конституэнты единицы, а значит, в ее СДНФ должно быть четыре слагаемых. Результат будет следующий: m(x1,x2,x3)=x1x2x3 +x1x2x3 +x1x2x3 +x1x2x3 Аналогично строится СКНФ. Выбираем конституэнты нуля и для каждой составляем элементарную дизъюнкцию. Получим: m(x1,x2,x3)=(x1 +x2 +x3)(x1 +x2 +x3)(x1 +x2 +x3)(x1 +x2 +x3). #

Полнота стандартного базиса позволяет подбирать и другие полные системы функций. Полнота множества F может быть установлена из следующих соображений. Предположим, каждая из трех функций стандартного бузиса представима формулой над F . Тогда в силу теоремы 1.3 иножество F будет полным.

Пример 1.3. Множество из операций сложения по модулю 2, умножения и константы 1 называют базисом Жегалкина. Сложение по модулю 2 и умножение — базовые операции кольца Z2, выражения, составленные с их помощью — это многочлены над кольцом Z2. Кон- станта 1 в данном случае необходима для записи свободного члена. Поскольку xx = x, то все сомножители в многочлене имеют степень 1. Поэтому при записи многочлена можно обойтись без понятия степени. Примеры формул над базисом Жегалкина:

xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.

Любую такую формулу называют полиномом Жегалкина. Фактически полином Жегалкина — это многочлен над кольцом Z2.

Нетрудно сконструировать формулы над базисом Жегалкина, представляющие операции сложения и отрицания стандартного базиса (умножение у двух базисов общее):

x+y=x⊕y⊕xy, x=x⊕1.

Поэтому базис Жегалкина — полное множество.
Можно показать, что для любой булевой функции полином Жегалкина определен однозначно

(точнее, с точностью до порядка слагаемых). Коэффициенты полинома Жегалкина при небольшом количестве переменных можно найти методом неопределенных коэффициентов.

Пример 1.4. Рассмотрим множество из единственной функции — штриха Шеффера*. Это множество полно, что следует из следующих легко проверяемых тождеств:

x=x|x, xy=x|y=(x|y)|(x|y), x+y=x|y=(x|x)|(y|y).

Пример 1.5. Базис, состоящий из единственной функции — стрелки Пирса, также является полным. Проверка этого аналогична случаю штриха Шеффера. Впрочем, это заключение можно сделать и на основании принципа двойственности для симметричных полуколец.

*Штрих Шеффера — бинарная, но не ассоциативная операция. Поэтому при использовании инфиксной формы следует быть внимательным: результат зависит от порядка выполнения операций. В этом случае рекомендуется явно указывать порядок операций при помощи скобок, например писать (x | y) | z, а не x | y | z, хотя обе формы равнозначны.