Булевы алгебры
ТеорияБулева алгебра: симметричное полукольцо с унарной операцией дополнения x → x с аксиомами x + x = 1, x x = 0. Единственность дополнения. Булевы алгебры и булевы кольца. Булева алгебра как решетка. Решетка — алгебра (L, ∨, ∧) в которой операции (hешеточные объединение и пересечение) ассоциативны, коммутативны, идемпотентны и связаны тожде- ствами поглощения a ∨ (a ∧ b) = a, a ∧ (a ∨ b) = a. Всякое симметричное полукольцо является решеткой, а дистрибутивная решетка (каждая операция дистрибутивна относительно другой) с нулем и единицей — симметричным полукольцом. Пример булевой алгебры — булев куб Bn. Теорема: любая конечная булева алгебра изоморфна булеву кубу некоторой размерности.
Напомним, что по определению булева алгебра — это симметричное полукольцо, в котором введена еще одна унарная операция — дополнение. Дополнение элемента x, обозначаемое x, удовлетворяет аксиомам x + x = 1, x x = 0. Отметим, что эти два равенства для любого x определяют элемент x однозначно, т.е. существование дополнения определяется свойствами двух бинарных операций.
Подробнее можно сказать, что булева алгебра — универсальная алгебра вида (L, {+, ·, }), удовлетворяющая условиям:
а) каждая бинарная операция коммутативна, ассоциативна, идемпотентна и имеет нейтраль- ный элемент;
б) каждая бинарная операция дистрибутивна относительно другой;
в) нейтральный элемент каждой бинарной операции является аннулирующим другой бинар- ной операции;
г) дополнение связано с бинарными операциями аксиомами x + x = 1, x x = 0.
Обе операции порождают два отношения порядка, являющиеся взаимно обратными. Так, отношение x y, равносильное равенству x + y = y, также определяется равенством xy = x.
Если в булевой алгебре B ввести операцию x ⊕ y = xy + xy, то получим алгебраическую систему (L, {⊕, ·}), которая является кольцом с единицей, в котором операция умножения идемпотентна (булевым кольцом). Короче говоря, булева алгебра является булевым кольцом. Наоборот, в любом булевом кольце (L, {⊕, ·}) умножение коммутативно, а сложение удовлетворяет условиюx⊕x=0. Положив x+y=x⊕y⊕xy, x=x+1,получималгебраическуюсистему (L, {+, ·, }), представляющую собой булеву алгебру.
К понятию булевой алгебры можно подойти и с другой стороны. Коммутативная идемпо- тентная полугруппа называется полурешеткой. В полурешетке (как и в полукольце) можно ввести отношение естественного порядка согласно правилу x y ⇔ x+y = y. Наоборот, любое упорядоченное множество, в котором любое двухэлементное множество имеет точную верхнюю грань, можно интерпретировать как полурешетку с операцией x + y = sup {x, y}. Если в упо- рядоченном множестве каждое двухэлементное множество имеет и точную верхнюю, и точную нижнюю грани, то на это множестве можно ввести структуру полурешетки двумя способами: с операцией sup {x, y} и с операцией inf {x, y}. Первую структуру называют верхней полуре- шеткой, а вторую — нижней. Две решеточные операции связаны тождествами
sup {x, inf {x,y}} = x, inf {x, sup{x,y}} = x.
Алгебра (R, {∨, ∧}), для которой (R, ∨) и (R, ∧) есть полурешетки, причем операции связаны тождествами поглощения a ∨ (a ∧ b) = a, a ∧ (a ∨ b) = a, называется решеткой. Бинарные операции называются решеточными (решеточное объединение и решеточное пересечение). Решеточные операции входят в структуру решетки симметрично. Поэтому любую из них можно назвать объединением, тогда втораябудет пересечением. Структуру решетки имеет любое упорядоченное множество, в котором для любого двухэлементного множества существует точная верхняя и точная нижняя грани. В этом случае решеточными операциями будут a∨b=sup{a, b} и a∧b=inf {a, b}.
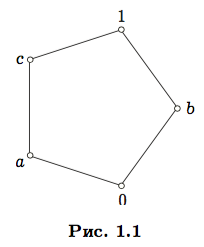 |
Структуру решетки имеет любое симметричное полукольцо. Решетка в общем случае может и не быть симметричным полукольцом. Например, пентагон — упорядоченное множество {0, a, b, c, 1} с отношением порядка, заданным диаграммой Хассе* на рис. 1.1, — является решеткой, но в этой решетке операции не являются дистрибутивными друг относительно друга, как должно быть в симметричном полукольце. Однако всякая дистрибутивная решетка (т.е. решетка, в которой каждая операция дистрибутивна относительно другой) с нулем и единицей (нейтральными элементами объединения и пересечения) является симметричным полукольцом. |
Простейший пример булевой алгебры — двухэлементная булева алгебра
B=({0, 1}, {+, ·, })
с операциями x+y = max {x, y}, xy = min{x, y}, x = x+1. Обобщением этого примера является булева алгебра Bn с покомпонентным выполнением операций алгебры B на кортежах. Алгебру Bn называют n-й декартовой степенью B или n-мерным булевым кубом. Оказывается, что любая конечная булева алгебра изоморфна некоторому булеву кубу. Попросту говоря, других примеров конечных алгебр, отличных от булева куба, нет.
Другой важный пример булевой алгебры — алгебра SA = 2A, {∪, ∩, } , т.е. множество всех подмножеств множества A с теоретико-множественными операциями объединения, пересечения и дополнения. Отметим, что все практически значимые примеры булевых алгебр можно интерпретировать в рамках алгебры SA или какой-либо ее подалгебры. Например, элементы булевой алгебры Bn (n-мерные булевы векторы) можно рассматривать как запись характеристической функции подмножества в множестве из n элементов. А тогда операции в Bn будут соответствовать теоретико-множественным операциям. Симметричное полукольцо ([a, b], {max, min}) можно преобразовать в алгебру множеств, поставив в соответствие каждому x ∈ [a, b] отрезок [a, x]. Множество таких отрезков замкнуто относительно операций объединения и пересечения, т.е. образует подалгебру в 2[a,b]. Правда это полукольцо не является булевой алгеброй, так как в нем нельзя ввести операцию дополнения.