Циклы, разрезы и задача Эйлера

Эйлеровы цепи и циклы. Циклы в графе. Фундаментальные циклы, числа Бетти. Разрезы. Критерий существования. Приложения.

Эйлеровы графы. Обнаружение замкнутых цепей, и в частности циклов — важная задача в исследовании графов. Во-первых, циклы в графе — существенная характеристика структуры этого графа. Во-вторых, наличие циклов влияет на многие алгоритмы на графах. Например, циклы отрицательного веса могут привести к тому, что задача о кратчайших путях не будет иметь решения.

Одной из задач теории графов, фактически положившей начало этой теории, является задача обнаружения эйлеровых циклов и эйлеровых цепей. Эйлеров цикл — это закнутая цепь, которая проходит через каждое ребро графа и притом один раз. Эйлеров цикл может не быть циклом в нашем понимании, так как некоторые вершины могут проходится несколько раз. В этом случае мы введем в обиход термин квазицикл, т.е. любая замкнутая цепь, в которой ребра не повторяются. Отметим, что вершины, не попадающие в эйлеров цикл, являются изолированными. Мы этот случай рассматривать не будем и дополним определение эйлерова цикла требованием, что каждая вершина попадает в эйлеров цикл.

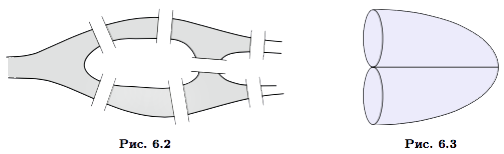
Понятие эйлерова цикла имеет прямое отношение к задачам прорисовки фигур без отрыва карандаша от бумаги. Другой исторической задачей является задача о Кенигсбергских мостах, изучавшаяся Л. Эйлером и приведшая к понятию эйлерова цикла. Задача состояла в обходе Кенигсберга с условием, что каждый мост проходится ровно один раз (рис. 6.2). Рассма- тривая разделенные участки суши как вершины графа, а соединяющие эти участки мосты — как ребра (рис. 6.3), приходим к задаче поиска такой цепи в графе, которая содержит каждое ребро, и притом один раз, т.е. к задаче поиска эйлеровой цепи.

Любой квазицикл можно разделить на несколько циклов, возможно, имеющих общие вершины, но не имеющих общих ребер. Действительно, начав перемещение по квазициклу мы получим последовательность вершин a₁, a₂, ..., a_k, a_i, где i < k. Поскольку в цепи ребра не повторяются, последовательность вершин a_i, a_i+1, . . . , a_k есть цикл. Выделим этот цикл, а маршрут движения сократим: a₁, a₂, . . . , a_i−1, a_i, a_k. Повторяя эту процедуру и учитывая, что количество вершин в цикле конечно, мы придем к набору циклов с общими вершинами, но без общих ребер.

 

Теорема 6.4. Граф G имеет эйлеров цикл тогда и только тогда, когда он связен и любая его вершина имеет четную степень.

◀ Отметим, что оба отмеченных условия (связность и четность степеней) необходимы для существования эйлерова цикла, поскольку при движении по циклу мы попадаем в каждую вершину и выходим. В результате, во-первых, цикл соединяет все вершины, что обеспечивает связность графа. А во-вторых, для каждой вершины инцидентные ребра разделяются на пары, в каждой из которых одно ребро входящее, а другое выходящее. Поэтому степени всех вершин четные.

Предположим, что граф связен, а все вершины имеют четную степень. Выберем произвольную вершину v₀ и начнем движение по графу по любому инцидентному ребру. Это движение не может закончиться в вершине, отличной от стартовой, поскольку четная степень вершины гарантирует, что если мы пришли в нее, то есть хотя бы одно не использовавшееся ребро. Поэтому в такой вершине цепь можно продолжить, обеспечивая неповторяемость ребер. В то же время в силу конечности множества всех ребер цепь в какой-то момент должна закончиться. Это может произойти только в тот момент, когда мы вернемся в стартовую вершину и не окажется ни одного инцидентного ребра, которое еще не использовалось.

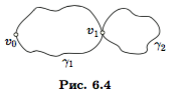
Обозначим полученный квазицикл γ₁. Предположим, что в этот квазицикл входят не все ребра графа. Тогда должно быть хотя бы одно ребро, не вошедшее в квазицикл γ₁, инцидентное одной из вершин v₁ этого квазицикла (в противном случае мы имеет несвязный граф). Отметим, что после удаления квазицикла γ₁ все вершины графа будут иметь четную степень. Начинаем движение из вершины v₁ по ребрам, не вошедшим в γ₁. Рассуждая как и выше, заключаем, что движение закончится в вершине v₁, и мы получаем квазицикл γ₂, не имеющий с γ₁ общих ребер, но имеющий с ним общую вершину v₁. Эти два квазицикла можно объединить в один квазицикл γ₂ (рис. 6.4). Если объединенный квазицикл охватывает не все ребра графа, мы опять можем выбрать вершину v₁ этого квазицикла, у которой есть незадействованные инцидентные ребра, и, начиная движение из вершины v₁, построить следующий квазицикл γ₃. Присоединяем квазицикл γ₃ к γ₂ . Этот процесс продолжаем далее. Он завершится тогда, когда не останется незадействованных ребер. В результате будет получен квазицикл, содержащий все ребра графа, т.е. эйлеров цикл. ▶

Следствие 6.2. Для того чтобы граф G имел эйлерову цепь, необходимо и достаточно, чтобы он был связен, две его вершины имели нечетную степень, а остальные — четную.

◀Пусть вершины v₁ и v₂ имеют нечетную степень. Если эти вершины несмежные, добавим к графу ребро γ, соединяющее v₁ и v₂. Получим связный граф, у которого все вершины имеют четную степень. Такой граф имеет эйлеров цикл. Удалив из эйлерова цикла ребро γ, получим эйлерову цепь исходного графа.

Если вершины v₁ и v₂ смежные, мы можем добавить к графу еще одну вершину v′, соединив ее с вершинами v₁ и v₂. Опять в расширенном графе существует эйлеров цикл, который после удаления дополнительной вершины и двух ребер становится эйлеровой цепью исходного графа. ▶

Фундаментальные циклы. Отметим две характеристики графа, условно противоположные друг другу: несвязность и существование циклов. Для связного графа количество ребер, при которых могут отсутствовать циклы, ограничено (n−1 ребро). При увеличении количества ребер появляются циклы, при уменьшении — теряется связность.

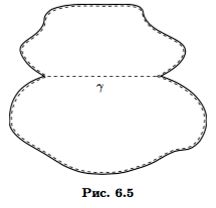
Пусть граф G связный. Выберем в нем остовное дерево T. Добавление к T одного ребра графа G приводит к появлению одного цикла. В самом деле, если добавляемое ребро γ входит в два цикла, то объединяя циклы, но уже без γ, получим цикл в дереве T (рис. 6.5). Поскольку дерево не имеет циклов, то и предположение о появлении в связи с γ двух циклов оказывается ложным.

Итак, выбор в графе G остовного дерева разделяет все ребра графа на две группы: древес- ные ребра, вошедшие в остов, и обратные ребра, не вошедшие в остов. С каждым обратным ребром графа связан вполне определенный цикл графа G. Совокупность этих циклов образует фундаментальную систему циклов. Основным ее свойством является то, что с помо- щью фундаментальной системы циклов можно построить любой цикл графа, в то время как ни один из циклов фундаментальной системы не выражается через другие. Это похоже на ситуацию в линейном пространстве при рассмотрении понятия базиса. Отметим, что ассоциация с линейной алгеброй оказывается весьма содержательной и не является поверхностной.

Любую цепь в графе без повторений ребер (полупростую цепь) можно интерпретировать как некоторой множество ребер этого графа. Если из данной совокупности ребер графа можно сложить полупростую цепь, то такая цепь единственна (если, конечно, не различать цепи из одних и тех же ребер, но с противоположной ориентацией). Другими словами, множество всех цепей графа можно рассматривать как подмножество булеана множества всех ребер графа G. Булеан множестува ребер с операцией симметрической разности представляет собой абелеву группу, причем в этой группе каждый элемент является противоположным самому себе. Такая абелева группа может рассматриваться как линейное пространство над полем Z₂. В результате мы приходим к понятию пространства цепей графа. В этом линейном пространстве рассмотрим линейную оболочку всех циклов. Получим пространство циклов графа. Наша цель — показать, что фундаментальная система циклов есть базис в пространстве циклов графа.

Отметим, что пространство циклов содержит все квазициклы, так как каждый квазицикл есть сумма нескольких циклов.

Теорема 6.5. Сумма двух квазициклов есть либо пустое множество, либо квазицикл, либо объединение нескольких попарно непересекающихся квазициклов.

◀Рассмотрим общие вершины двух циклов. В сумме степеней каждой вершины, относящихся к каждому из квазициклов, общие ребра считаются дважды. Поэтому после удаления общих ребер, т.е в результате суммирования, мы из двух квазициклов получим граф, у которого все вершины имеют четные степени. Это означает, что каждая компонента связности такого графа есть эйлеров граф, или квазицикл. Значит, сумма двух квазициклов есть объединение не пересекающихся квазициклов.▶

Теорема 6.6. Фундаментальная система циклов, порожденная выбранным остовом, является базисом в пространстве циклов связного графа.

◀Фундаментальная система циклов линейно независима в пространстве циклов. В самом деле, выберем и приравняем нулю произвольную линейную комбинацию α₁c₁ +α₂c₂ +. . .+α_kc_k циклов c₁, c₂, . . . , c_k с коэффициентами α_i ∈ Z₂. Цикл c1 имеет обратное ребро r₁, которое не входит ни в какой другой цикл. Значит, равенство нулю линейной комбинации возможно только при α₁ = 0. Повторяя рассуждения для всех остальных циклов линейной комбинации, заключаем, что все коэффициенты линейной комбинации равны нулю.

Пусть c₁, c₂, . . . , c_k — фундаментальная система циклов, причем каждый цикл c_i связан с обратным ребром γ_i. Выберем произвольный цикл c. Пусть этот цикл содержит обратные ребра r_i1, r_i2, ..., r_il. Тогда множество c △ c_i1 △ c_i2 △ ... △ c_il не содержит обратных ребер, а следовательно, состоит из ребер, принадлежащих остову. Это множество как сумма нескольких циклов, либо пусто, либо является объединением некоторого набора не пересекающихся квазициклов, а значит, набора циклов, не имеющих общих ребер. Однако в остовном дереве вообще нет циклов. Поэтому указанная сумма есть пустое множество, т.е.

c △ c _i1 △ c_i2 △ . . . △ c_il = ∅.

Это равенство эквивалентно равенству

c = c_i1 △ c_i2 △ . . . △ c_il,

поскольку в пространстве циклов каждый элемент является противоположным самому себе.

Таким образом, любой цикл графа является линейной комбинацией фундаментальной системы циклов. Следовательно, фундаментальная система циклов — базис в пространстве циклов графа.▶

Доказанная теорема позволяет определить размерность пространства циклов по числу обратных ребер. Если n — число вершин связного графа, m — число его ребер, то размерность пространства циклов равна m − n + 1.

Понятие пространства циклов можно ввести и для несвязного графа. В этом случае любой цикл (квазицикл) есть цикл (квазицикл) одной из компонент. Остов графа будет лесом, но при этом сохраняется свойство, что любое обратное ребро порождает ровно один цикл. Таким образом, пространство циклов имеет размерность m−n+p, где p — число компонент связности.

Размерность пространства циклов, равная c(G) = m − n + p, называется цикломатическим числом графа. Число ν(G) = n − p, равное числу ребер в остове графа, называется коцикломатическим числом. Обе эти характеристики — инварианты, которые могут ис- пользоваться при анализе графов на изоморфность.

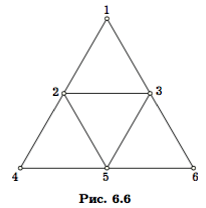
Отметим, что не любой базис пространства циклов можно получить исходя из некоторого остова этого графа. Фундаментальная система циклов обладает следующим свойством: каждый цикл фундаментальной системы имеет ребро, при удалении которого разрывается только один цикл. Для графа на рис. 6.6 цикломатическое число равно 4. Нетрудно увидеть четыре независимых цикла этого графа: 1−2−3, 2−4−5, 2−3−5, 3−5−6. Сумма двух, трех или всех четырех циклов не может быть равна нулю, поскольку у трех циклов из четырех есть ”персональные“ ребра. В то же время у внутреннего цикла ребра таковы, что удаление любого из них разрывает сразу два цикла из четырех. Это означает, что рассмотренная система циклов не порождается каким-либо остовом.

Для построения фундаментальной системы циклов следует выполнить следующие шаги.

1. построить остов графа (дерево или лес);

2. разделить все ребра графа на древесные и обратные;

3. для каждого обратного ребра построить соответствующий ему цикл. Для этого в остове необходимо найти единственную цепь, соединяющую концы ребра, и к этой цепи добавить само ребро.

Фундаментальные разрезы. Разделим вершины графа произвольным образом на две группы и выберем в графе множество тех ребер, которые соединяют вершины разных групп. Это множество может быть пустым (это произойдет в том случае, если каждая компонента связности целиком попадает в одну из групп). Если же оно не пустое, то удаление ребер множества из графа увеличивает его связность. Описанное множество называется разрезом графа.

Изучение разрезов позволяет оценить важные свойства графа. Например, анализ разрезов графа городских дорог позволяет найти узкие места в организации транспортных потоков и найти выверенные решения по развитию сети дорог.

Вообще, под разрезом можно было бы понимать любое множество ребер графа, удаление которых повышает связность этого графа. Однако такое определение не эквивалентно предыдущему, оно является расширением понятия разреза. В самом деле, в графе на рис. 6.6 выберем множество из трех ребер {1, 2}, {1, 3}, {2, 3}. Удаление этих ребер делает граф несвязным (вершина 1 становится изолированной). Однако не существует такого разделения вершин на две группы, при котором концы все трех ребер будут принадлежать разным группам. Множество ребер, удаление которых повышает связность графа, будем называть разделяющим множеством. Разрез — частный случай разделяющего множества.

Множество всех разрезов графа можно рассматривать как полугруппу с операцией объеди- нения (точнее, совокупность всех разрезов в реберном булеане графа с операцией объединения порождает некоторую подполугруппу). Поскольку объединение — идемпотентная операция, алгебра разрезов есть полурешетка, отношение порядка которой совпадает с отношением включения множеств. Интересна база этой алгебры, т.е. минимальное множество разрезов, по- рождающее всю алгебру разрезов. Естественно к базе разрезов относить только минимальные разрезы, т.е. такие разрезы, которые не содержат подмножеств, также являющихся разрезами (такие разрезы также называют простыми разрезами).

Условие минимальности позволяет стереть границу между разрезом и разделяющим мно- жеством: минимальное разделяющее множество оказывается разрезом. Отметим, что минимальное разделяющее множество состоит из ребер лишь одной компоненты связности графа. Увеличение связности означает, что хотя бы одна из компонент связности графа разделяется на большее число компонент. Очевидно, что можно ограничиться множеством ребер, входящих только в эту разделяемую компоненту. В свете этого можно ограничиться рассмотрением частного случая связного графа.

Теорема 6.7. Любое минимальное разделяющее множество связного графа разделяет граф точно на две компоненты и тем самым определяется некоторым разделением вершин графа на два множества (т.е. является разрезом).

◀Предположим, что граф разделился на три или большее число компонент. Поскольку изна- чально граф был связным, в разрез входит ребро, соединяющее первую компоненту (при любой изначально выбранной нумерации компонент) с какой-то другой. Удаление этого ребра из разделяющего множества приводит к слиянию двух компонент, но оставляет граф несвязным.

Таким образом, мы приходим к другому разделяющему множеству, которое является подмножеством рассматриваемого разделяющего множества. Это противоречит условию минимальности разделяющего множества.

Минимальное разделяющее множество делит граф в точности на две компоненты G₁ и G₂, разделяя тем самым множество вершин графа на две группы V₁ и V₂. Очевидно, что рассматриваемое разделяющее множество содержит все ребра, соединяющие вершины из V₁ с вершинами из V₂, а в силу минимальности не содержит никаких других ребер. Значит, рассматриваемое разделяющее множество порождается группами вершин V₁ и V₂ и является разрезом.

Теорема 6.8. Любой разрез графа можно представить как объединение минимальных разрезов.

◀Чтобы доказать сформулированное утверждение, нужно показать, что любое ребро рассматриваемого разреза входит в некоторый минимальный разрез, являющийся частью рассматри- ваемого разреза. Из этого факта сразу вытекает, что любой разрез есть объединение минимальных разрезов, подчиненных данному.

Как и выше, можем ограничиться случаем связного графа G = (V, E). Рассмотрим некоторое ребро γ разреза R, соединяющее вершины v₁ и v₂. Рассмотрим вспомогательный граф, вершинами которого являются компоненты связности графа (V, E \ R) (графа G без разреза R), полагая, что две такие компоненты соединены ребром, если в разрезе есть ребро, соединяющее вершины двух компонент связности. Этот вспомогательный граф называют конденсацией графа G. Так как любые две вершины одной компоненты связности достижимы друг из друга, то связь между двумя компонентами связности можно провести по любому ребру, соединяющему вершины этих компонент. Возникает отношение эквивалентности на ребрах графа G, причем каждому классу эквивалентности будет соответствовать одно ребро конденсированного графа.

В силу построения разрез состоит из некоторого множества упомянутых выше классов эквивалентных ребер. Удаление разреза приводит к тому, что конденсированный граф становится графом без ребер. Отметим, что любую цепь в конденсированном графе, соединяющую компоненты с вершинами v₁, v₂ можно детализировать так, что получится цепь, соединяющая в исходном графе вершины v₁, v₂.

Из этих рассуждений вытекает, что минимальный разрез графа G, подчиненный разрезу R представляет собой объединение нескольких классов эквивалентности, а потому соответствует некоторому разрезу конденсированного графа.

Поскольку разрез порождается двумя множествами вершин V₁ и V₂, конденсированный граф будет состоять из двух групп вершин (компонент связности, попадающих в V₁ или V₂), причем ребра графа будут соединять вершины разных групп (такой граф называется двудольным ). Пусть Γ — класс эквивалентности, содержащий ребро γ. Покажем, что Γ является частью некоторого минимального разреза конденсированного графа. Этот разрез порождает минимальный разрез исходного графа, подчиненный разрезу R. Пусть v ̃₁ и v ̃₂ — вершины конденсированного графа, соответствующие вершинам v₁ и v₂ исходного.

Выберем совокупность тех ребер конденсированного графа, инцидентных v ̃₁, которые являются началом цепи из вершины v ̃₁ в вершину v ̃₂. Эта совокупность является разделяющим множеством конденсированного графа, поскольку его вершины v ̃₁ и v ̃₂ после удаления множества ребер оказываются недостижимыми друг из друга. В то же время эта совокупность — минимальное разделяющее множество, поскольку для любых двух вершин есть цепь, соединяющая их. Удаляемое множество ребер либо не затрагивает указанную цепь, либо эта цепь проходит через tildev1. Но тогда либо восстанавливаемое ребро восстанавливает и всю цепь, либо восстановленное ребро позволяет по этому ребру попасть в вершину v ̃₂, а затем вернувшись к вершине, соседней с v ̃₁, затем построить альтернативную цепь. Значит, сокращение количества ребер в разделяющем множестве восстанавливает связность.

Поскольку минимальное разделяющее множество есть простой разрез, любое ребро разреза R будет входить в некоторый простой разрез, целиком входящий в R. ▶

Систему минимальных разрезов, порождающих алгебру разрезов, можно строить, используя остов графа. Поскольку любые вершины связного графа можно соединить цепью в пределах остова графа, любой разрез графа должен быть и разрезом остова. Разрезы дерева устроены просто: минимальным разрезом дерева является любое ребро, поскольку удаление ребра в дереве автоматически делает это дерево несвязным.

Из этого рассуждения вытекает, что любой разрез графа должен содержать хотя бы одно древесное ребро. Можно построить систему разрезов, каждый из которых содержит ровно одно древесное ребро. Достаточно к этому древесному ребру добавить обратные ребра всех содержащих его фундаментальных циклов. Любая простая цепь, соединяющая концы древесного ребра есть часть цикла, содержащего это ребро. Но любой цикл есть сумма фундаментальных циклов, а потому содержит одно из выбранных обратных ребер. Следовательно, любая простая цепь, соединяющая концы древесного ребра, окажется разорванной, а граф станет несвязным. Ясно, что указанное разделяющее множество минимально, так как удаление из него любого ребра восстанавливает одну из цепей, связывающей две вершины. Граф возвращает свою связность.

Построенная система разрезов называется фундаментальной системой разрезов. В фундаментальной системе разрезов каждый элемент — минимальный разрез. Однако отсюда не следует, что любой разрез графа может быть получен как объединение некоторых разрезов фундаментальной системы. Например, треугольник с вершинами 1, 2, 3 и ребрами γ₁ = {1, 2}, γ₂ = {1, 3}, γ₃ = {2, 3} (например, подграф графа на рис. 6.6, порожденный вершинами 1, 2, 3) имеет остов с двумя ребрами γ₁ и γ₂. Фундаментальную систему разрезов образуют пары ребер {γ₁, γ₃} и {γ₂, γ₃}. Разрез {γ₂, γ₃} также минимальный, но не является объединением предыдущих двух.