Задача о путях в размеченном графе
ТеорияОтношение достижимости и матрица достижимости. Граф как отношение (отношение смежности) и транзитивное замыкание. Понятие о размеченном графе. Сведение задачи к вычислению итерации матрицы в полукольце. Алгоритм Дейкстры. Алгоритм Флойда.
Граф G = (V, E), у которого каждой вершине приписан вес, называется размеченным графом. К размеченным графам может относиться сеть дорог, каждая из которых имеет оценку качества и протяженности. Для такой сети актуальна задача поиска оптимального маршрута. Размеченный граф может обозначать финансовые потоки между различными составляющими бизнес-процесса, информационные потоки в компьютерной сети и т.п.
Задача о путях в размеченном графе может формулироваться в трех вариантах:
• найти кратчайшую цепь, связывающую две заданные вершины графа;
• для заданной вершины v0 построить кратчайшие цепи, соединяющие v0 со всеми остальными вершинами графа;
• построить кратчайшие цепи для всех пар вершин графа.
Задача может ставиться как для неориентированных, так и для ориентированных графов. Под весом цикла (пути) понимается сумма весов всех ребер (дуг), входящих в цепь (путь). Однако важно то, что понятие ”сумма“ может меняться. Фактически весами в графе могут быть элементы любого полукольца или кольца. Например, как частный случай поставленной задачи можно рассматривать задачу построения матрицы достижимости для данного графа. Достаточно разметить граф над полукольцом B, причем под суммой понимать произведение в B. Тогда вес каждой цепи будет равен 1, а матрица весов кратчайших путей будет совпадать с матрицей достижимости.
Требование, чтобы веса графа были элементами полукольца, вообще говоря, не является обя- зательным. Достаточно обеспечить алгоритм, позволяющий по весам звеньев цепи однозначно определить вес всей цепи.
В результате решения общей задачи мы для каждой пары вершин v и w получаем значение наименьшего веса цепи (пути), соединяющей v и w, которое называется стоимостью. Из стоимостей можно составить матрицу стоимостей. Процесс решения задачи состоит в вычислении матрицы стоимостей.
Отметим, что наличие в графе, размеченном над кольцом R, циклов (контуров) отрица- тельного веса может привести к тому, что задача не будет иметь решения. В этом случае необходимо исключить из рассмотрения такие циклы или по крайней мере ограничить число проходов по ним.
Решение первого и второго вариантов задачи как часть входит в решение третьего варианта. Выделение их как самостоятельных преследует цель выбора специальных более экономичных алгоритмов для их решения.
Остановимся на первом варианте задачи.
Алгоритм Дейкстры. Этот алгоритм рассчитан на случай, когда в графе все веса неотрицательные. Он позволяет для заданной вершины v0 ориентированного графа построить стоимости D[v] для каждой пары вершин v0 и v. Алгоритм сводится к построению последовательности S1, S2, . . . , Sn множеств вершин, в которой множество Sk+1 получается из Sk добавлением одной вершины, и вычислению для каждого множества Sk множества Dk[v] стоимостей, определяемых только по тем путям из v0 в v, которые не выходят за пределы множества Sk (за исключением конечной вершины v). Начальное множество S1 состоит из единственной вершины v0, а массив стоимостей D1[v] — из весов дуг, связывающих вершину v0 с вершиной v. При отсутствии дуги, связывающей v0 с v, полагаем D1[v] = ∞. На каждом шаге алгоритма к множеству Sk добавляется вершина w = vv+1 ∈/ Sk, для которой значение Dk[w] является наименьшим. Затем вычисляется массив Dk+1[v] с помощью следующей процедуры пересчета. Если v ∈ Sk+1, то Dk+1[v] = Dk[v]. Если же v ∈/ Sk+1, то в качестве Dk+1[v] выбирается наименьшее из значений Dk[v] и Dk[vk+1] + ω(vk+1, v]), где ω(v, w) — вес дуги, соединяющей вершины v и w.
Через n шагов алгоритма Дейкстры множество Sk будет содержать все вершины графа, а массив Dk[v] — стоимости пар вершин v0, v. При реализации на практике массивы Dk[v] можно совместить. При этом на k-м шаге общий массив D[v] будет содержать значения Dk[v]. При пересчете значения D[v] для вершин v ∈ Sk+1 не изменяются, пересчитываются лишь те, для которых v ∈/ Sk+1.
Как видим, алгоритм Дейкстры ориентирован на решение второго варианта задачи о путях. Однако его легко модифицировать для решения и первого варианта задачи: достаточно процесс остановить в тот момент, когда в качестве вершины vk+1 будет выбрана заданная конечная вершина пути.
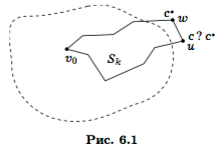
Почему алгоритм Дейкстры приводит к кратчайшему пути. Выбор на каждом шаге точки Vk+1, путь к которой (из обследованных в рамках множества Sk) является кратчайшим, позволяет сразу объявить этот путь кратчайшим и во всем графе. Это вытекает из следующих соображений. Пусть на k-м шаге в вершину w ведет кратчайший путь веса c∗, т.е. Dk[w] = c∗ и минимальна для всех вершин вне Sk (рис. 6.1). Рассмотрим другой путь, ведущий в w через некоторую вершину v. По условиям выбора c = Dk[v] ≥ c∗. Учитывая, что часть пути из v в w имеет неотрицательный вес, заключаем, что вес альтернативного пути не меньше, чем тот, по которому был вычислен вес Dk[v]. Как видим, явно используется условие неотрицательности весов графа. Отметим, что это условие автоматически выполнено, если граф размечен над идемпотентным полукольцом. Можно также условие неотрицательности весов заменить условиекм монотонности: вес любого пути не должен быть меньше веса любой своей части.
Алгоритм Дейкстры по своей сути — процедура перебора путей в графе для отбора среди них оптимальных. Эту процедуру легко модифицировать так, чтобы можно было получать не только веса оптимальных путей, но и сами эти пути, т.е. пути наименьшего веса. Достаточно в качестве значений массива D[v] рассматривать не стоимости пар вершин, а векторы, первой компонентой которых является вес оптимального пути (стоимость), а остальные компоненты описывают цепочку вершин, представляющую собой оптимальный путь из вершины v0 в вершину v. На k-м шаге при вычислении Dk+1[v] мы либо сохраняем вектор Dk[v], либо к первой компоненте вектора Dk[vk+1] добавляем вес ω(vk+1,v]), а к концу этого вектора присоединяем дугу, соединяющую вершины vk+1 и v.
Задача о путях в полукольцах. Во многих случаях в задаче о путях можно считать, что метки дуг (ребер) являются элементами некоторого полукольца. Выбор полукольца позволяет соответствующим образом интерпретировать понятие оптимальности пути.
Считаем, что весом пути является произведение (в полукольце) всех весов дуг, составляющих этот путь, а стоимостью пар вершин — сумма весов всех путей, соединяющих эти вершины. Рассмотрим задачу вычисления матрицы стоимости.
Обозначим через Ω матрицу весов графа. Тогда с учетом правила перемножения матриц заключаем, что Ω2 содержит стоимости пар вершин, вычисленные по всем путям длины 2, аналогично степень Ωk содержит стоимости пар вершин, вычисленные по всем путям длины k. Поскольку стоимость пары вершин определяется как сумма весов по всем путям, соединяющим эти вершины, заключаем, что матрица стоимости C определяется формулой
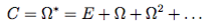
Здесь Ω∗ — итерация матрицы в рассматриваемом полукольце. Отметим, что в силу конечности графа любой путь длины больше n содержит цикл (контур) и содержит в себе как часть другой путь. Вес пути — произведение всех дуг. Следовательно, часть пути имеет больший вес и при суммировании поглощается. Это значит, что Ωn+1≤ Ωn. Поэтому
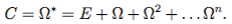
Если граф размечен обычными числовыми весами, достаточно в качестве умножения полукольца рассмотреть сложение действительных чисел, а в качестве сложения полукольца — минимум двух действительных чисел. Чтобы эта операция имела нейтральный элемент, достаточно ввести в рассмотрение вес ∞, обозначая им пары вершин, не связанные дугой графа. Вычисление минимума — коммутативная идемпотентная операция, относительно которой сложение дистрибутивно.
Анализ процедуры непосредственного вычисления Ω∗ показывает, что алгоритм сводится к методу динамического программирования.
Из теории полуколец вытекает, что итерация A∗ матрицы A может быть получена как решениематричногоуравненияX=AX+E.Вычислениеотдельногоj-гостолбцаxj матрицы X сводится к матричному уравнению xj = Axj + ej , где ej — j-й столбец единичной матрицы. А это матричное уравнение может интерпретироваться как матричная форма записи системы линейных уравнений.
Таким образом, вычисление матрицы стоимости сводится к решению нескольких систем линейных уравнений в некотором полукольце. В данном случае можно ограничиться вычислением одного столбца матрицы стоимостей, что равносильно вычислению массива D[v] стоимостей для пар вершин v и v0. Это можно реализовать как решение одной системы линейных уравнений над полукольцом.
Вычисление отдельных элементов матрицы Ω∗ можно свести к решению системы линейных уравнений над полукольцом. Решение такой системы осуществляется методом Гаусса (методом исключения неизвестных). Поскольку в конкретном рассматриваемом приложении требуется лишь один элемент матрицы Ω∗ (путь наименьшего веса, связывающий две данные вершины), то процедуру вычисления можно провести так, что в методе Гаусса будет использоваться только прямой ход (в системе нужно будет исключать последовательно все неизвестные, кроме того, которое определяется).
Прямое вычисление итерации матрицы весов (например, в случае, когда сложение — это минимум, а умножение — это обычное сложение) можно представить как последовательный пересчет матрицы весов по формуле
(6.1)
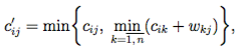
где cij — найденные стоимости, а wij — веса ребер. С одной стороны, видно, что это позволяет сравнить уже найденный минимальный маршрут длины m с маршрутом, проходящим через вершину k и тем самым получить минимальный маршрут длины m + 1. С другой стороны, в терминах полукольца указанный пересчет записывается так:
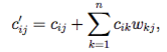
что в матричной форме равносильно равенству C ′ = C + C W . В итерационной C0 = E, Ck+1 = Ck + CkW мы через n шагов получим итерацию W∗ матрицы весов. процедуре
Описанный процесс вычисления итерации можно улучшать в разных направлениях. Нетрудно заметить, что итерацию можно получить по итерационной формуле Ck+1 = E + Ck W . Правда, с точки зрения объема вычислений это не дает преимуществ. Преимущество дает такой процесс: C1= E + W, C2 = C21 , C4 = C22 , C1 = C24 и т.д. Для вычисления итерации W∗ вместо n произведений достаточно вычислить log2 n квадратов.
Еще один прием связан с нарушением структуры матричных произведений (все матричные многочлены вычисляются параллельно). Оказывается, что для построения матрицы стоимо- стей в (6.1) можно не искать минимум по всем вершинам (минимум по k). Достаточно на каждом шаге использовать фиксированную вершину, меняя фиксированную вершину от шага к шагу. Точнее, на k-м шаге мы вычисляем
(6.2)
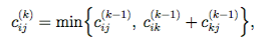
где C(0) = E. Через n шагов мы получим матрицу C(n), которая и будет являться матрицей стоимостей. Изложенный алгоритм был предложен Р. Флойдом.
Покажем, что алгоритм Флойда действительно приводит к минимальным весам маршрутов между любой парой вершин. Отметим, что на k-м шаге матрица Ck будет содержать для каждой пары вершин минимальные веса, получаемые по маршрутам, проходящим по первым k вершинам графа. Доказательство можно строить методом индукции. На старте в качестве C(0) выбираем матрицу E, имея в виду нуль и единицу соответствующего полукольца, т.е. в данном случае c (0() ij = 0 при i=j и (0() ij = ∞ при i̸=j. Очевидно,что эта матрица дает веса оптимальных маршрутов длины 0. Предположим, что матрица C(k−1) содержит веса оптимальных маршрутов, пролегающих по вершинам с номерами до k−1 включительно. Тогда формула (6.2) для вершин с номерами i и j выбирает наилучший маршрут среди ”старых“ веса c(k−1) и новых с дополнительной вершиной с номером k. В самом деле, наилучший маршрут, ij проходящий через k-ю вершину может состоять из двух оптимальных маршрутов, первый из i-й вершины в k-ю, второй из k-й вершины в j-ю. Через n шагов получим для каждой пары вершин вес оптимального маршрута без ограничений на включаемые вершины.