Предикаты

Решение задач

Определение. Предикатом называется повествовательное предложение, содержащее предметные переменные, определённые на соответствующих мно- жествах; при замене переменных конкретными значениями (элементами) этих множеств предложение обращается в высказывание, т. е. принимает значение «истинно» или «ложно».

Определение. Предикатом называется функция P : M n → B , где B = { 0,1 } , M - любое множество, 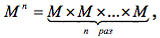т. е. функция P , сопоставляющая вектору (x1 , x2 ,..., xn ) значения 0 или 1.

Множество M называется предметной областью предиката P ,

x1 , x2 ,..., xn - предметные переменные,

P - предикатный символ,

n - местность предиката,

декартово произведение M × M × ... × M область определения предиката P .

Обозначение: P (x1 , x2 ,..., xn- n - местный предикат, заданный на множестве M .

Определение. Областью истинности предиката P называется подмножество Ip ⊆ Mn его предметной области, на элементах которого значения предиката равны 1.

Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями: IPvQ = IP ∪ IQ, IP ∧ Q = IP ∩ IQ , IP→Q = IP ∪ IQ, I P = IP .

Задача 3.1. Найти область истинности предиката

P ( X, Y ) = (( X + Y ) - нечётно ) ∨ (( X - Y ) делятся на 3) , где X = {1;3;6;7}, Y = {2;4;5}.

Решение.

Составим таблицы истинности для предикатов P1 ( X, Y ) = (( X + Y) - нечётно), P2( X, Y ) = (( X - Y ) - делятся на 3) , P = P1 ∨ P2.

IP = I P1∨P2 = IP1 ∪ IP2 = {(1,2), (1,4), (3,2), (3,4), (6,5), (7,2), (7,4)} ∪ {(1,4), (7,4)} = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.
Ответ: IP = {(1,2), (1,4), (3,2), (3,4), (6,4), (7,2), (7,4)}.

Задача 3.2. Найти область истинности предиката

P ( X ) = (( число 3 не делитель x ) → ( x ≤ 6 ))

на множестве однозначных натуральных чисел.

Решение.

Определим области истинности предикатов P1 = {число 3 не не делитель x},

P2 = {x ≤ 6}, P = P1→ P2 .

IP1 = {1,2,4,5,7,8}, IP2 = {1,2,3,4,5,6}, IP = IP1→P2 = IP1 = {1,2,3,4,5,6,9}.

Ответ: I P = {1,2,3,4,5,6,9}.

Задачи для самостоятельного решения

Найти область истинности предиката

  1. P ( X, Y ) = ((( X - Y ) - нечетно ) ∧ ( min ( X, Y)  - четно )), где X = {2;5;6;8};
  2. P ( X ,Y ) = (( X + Y )) - делится на 3) → (( X + Y ) > 5), где X = {2;5;6;8}, Y = {3;6;9};
  3. P ( X, Y ) = ((( X - Y ) - нечётно ) ∧ ( |Y-X| ≤ 1 )), где X = {5;8;9}, Y = {4;7;8;10};
  4. P ( X, Y ) = (( X - Y ) - чётно ) ∨ (( X + Y ) - делится на 3), где X = {5;8;9}, Y = {4;7;8;10};
  5. P ( X ) = (( число 3 делитель x ) ∨ ( x ≤ 6 )), заданного на множестве однозначных натуральных чисел;
  6. P ( X ) = ((( число 3 делитель x ) ∧ ( x > 6 )), заданного на множестве однозначных натуральных чисел;
  7. P ( X ) = (( x ≥ 3 ) ∧ ( x ≤ 10 )), заданного на множестве всех действительных чисел;
  8. P ( X ) = (( x2 ≤ 4 ) ∧ ( x -1 ≥ 1 )), заданного на множестве всех действительных чисел;
  9. P ( X ) = (( x ≤ 0 ) ∧ ( x2 - 2x ≤ 0 )), заданного на множестве всех действительных чисел;
  10. P ( X ) = (( x3 - 6x2 +11x - 6 = 0 ) ∧ ( x2 - 4x + 3 = 0 )),заданного на множестве всех действительных чисел.