Бинарные отношения. Операции над бинарными отношениями.
Решение задачОпределение. Бинарным отношением R называется подмножество пар (a,b)∈R декартова произведения A×B, т. е. R⊆A×B . При этом множество A называют областью определения отношения R, множество B – областью значений.
Обозначение: aRb (т. е. a и b находятся в отношении R ). /
Замечание: если A = B , то говорят, что R есть отношение на множестве A .
Способы задания бинарных отношений
1. Списком (перечислением пар), для которых это отношение выполняется.
2. Матрицей. Бинарному отношению R ∈ A × A , где A = (a1 , a2 ,..., an), соответствует квадратная матрица порядка n , в которой элемент cij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между ai и aj имеет место отношение R , или 0, если оно отсутствует:
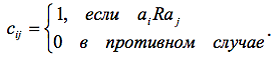
Свойства отношений
Пусть R – отношение на множестве A, R ∈ A×A . Тогда отношение R:
-
рефлексивно, если Ɐ a ∈ A: a R a (главная диагональ матрицы рефлексивного отношения содержит только единицы);
-
антирефлексивно, если Ɐ a ∈ A: a R a (главная диагональ матрицы рефле сивного отношения содержит только нули);
-
симметрично, если Ɐ a , b ∈ A: a R b ⇒ b R a (матрица такого отношения симметрична относительно главной диагонали, т.е. cij cji);
-
антисимметрично, если Ɐ a, b ∈ A: a R b & b R a ⇒ a = b (в матрице такого отношения отсутствуют единицы, симметричные относительно главной диагонали);
-
транзитивно, если Ɐ a, b, c ∈ A: a R b & b R c ⇒ a R c (в матрице такого отношения должно выполняться условие: если в i-й строке стоит единица, например в j-ой координате (столбце) строки, т. е. cij = 1 , то всем единицам в j-ой строке (пусть этим единицам соответствуют k е координаты такие, что, cjk = 1 ) должны соответствовать единицы в i-й строке в тех же k-х координатах, т. е. cik = 1 (и, может быть, ещё и в других координатах).
Задача 3.1. Определите свойства отношения R – «быть делителем», заданного на множестве натуральных чисел.
Решение.
отношение R = {(a,b):a делитель b}:
-
рефлексивно, не антирефлексивно, так как любое число делит само себя без остатка: a/a = 1 для всех a∈N ;
-
не симметрично, антисимметрично, например, 2 делитель 4, но 4 не является делителем 2;
-
транзитивно,таккакесли b/a ∈ N и c/b ∈ N, то c/a = b/a ⋅ c/b ∈ N, например, если 6/3 = 2∈N и 18/6 = 3∈N, то 18/3 = 18/6⋅6/3 = 6∈N.
Задача 3.2. Определите свойства отношения R – «быть братом», заданного на множестве людей.
Решение.
Отношение R = {(a,b):a - брат b}:
-
не рефлексивно, антирефлексивно из-за очевидного отсутствия aRa для всех a;
-
не симметрично, так как в общем случае между братом a и сестрой b имеет место aRb , но не bRa ;
-
не антисимметрично, так как если a и b –братья, то aRb и bRa, но a≠b;
-
транзитивно, если называть братьями людей, имеющих общих родителей (отца и мать).
Задача 3.3. Определите свойства отношения R – «быть начальником», заданного на множестве элементов структуры
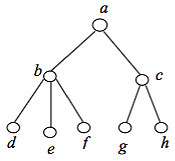
Решение.
Отношение R = {( a,b ) : a - начальник b}:
- не рефлексивно, антирефлексивно, если в конкретной интерпретации не имеет смысла;
- не симметрично, антисимметрично, так как для всех a≠b не выполняется одновременно aRb и bRa;
- транзитивно, так как если a начальник b и b начальник c , то a начальник c .
Задачи для самостоятельного решения
Определите свойства отношения Ri , заданного на множестве Mi матрицей, если:
- R1 «иметь один и тот же остаток от деления на 5»; M1 множество натуральных чисел.
- R2 «быть равным»; M2 множество натуральных чисел.
- R3 «жить в одном городе»; M3 множество людей.
- R4 «быть знакомым»; M4 множество людей.
- R5 {(a,b):(a-b) - чётное; M5 множество чисел {1,2,3,4,5,6,7,8,9}.
- R6 {(a,b):(a+b) - чётное; M6 множество чисел {1,2,3,4,5,6,7,8,9}.
- R7 {(a,b):(a+1) - делитель (a+b)} ; M7 - множество {1,2,3,4,5,6,7,8,9}.
- R8 {(a,b):a - делитель (a+b),a≠1}; M8 - множество натуральных чисел.
- R9 «быть сестрой»; M9 - множество людей.
- R10 «быть дочерью»; M10 - множество людей.
Операции над бинарными отношениями
Пусть R1, R1 есть отношения, заданные на множестве A .
-
объединение R1∪ R2 : R1 ∪ R2 = {(a,b) : (a,b) ∈ R1 или (a,b) ∈ R2} ;
-
пересечение R1∩ R2 : R1 ∩ R2 = {(a,b) : (a,b) ∈ R1 и (a,b) ∈ R2} ;
-
разность R1 \ R2 : R1 \ R2 = {(a,b) : (a,b) ∈ R1 и (a,b) ∉ R2} ;
-
универсальное отношение U: = {(a;b)/a ∈ A & b ∈ A}. ;
-
дополнение R1 U \ R1, где U = A × A;
-
тождественное отношение I : = {(a;a) / a ∈ A};
-
обратное отношение R-11 : R-11 = {(a,b) : (b,a) ∈ R1};
-
композиция R1 º R2 : R1 º R2 : = {(a,b) / a ∈ A&b ∈ B& ∃ c ∈ C : aR1 c & c R2b}, где R1⊂ A × C и R2⊂ C × B;
Определение. Степенью отношения R на множестве A называется его композиция с самим собой.
Обозначение: 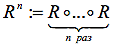
Определение. Если R ⊂ A × B , то R º R-1 называется ядром отношения R .
Теорема 3.1. Пусть R ⊂ A × A – отношение, заданное на множестве A .
Тогда:
- R рефлексивно тогда и только тогда, (далее используется знак ⇔) когда I ⊂ R.
- R симметрично ⇔ R = R-1.
- R транзитивно ⇔ R º R ⊂ R
- R антисимметрично ⇔ R ⌒ R-1 ⊂ I .
- R антирефлексивно ⇔ R ⌒ I = ∅ .
Задача 3.4. Пусть R - отношение между множествами {1,2,3} и {1,2,3,4}, заданное перечислением пар: R = {(1,1), (2,3), (2,4), (3,1), (3,4)}. Кроме того, S - отношение между множествами S = {(1,1), (1,2), (2,1), (3,1), (4,2)}. Вычислите R-1, S-1 и S º R. Проверьте, что ( S º R)-1 = R-1, S-1.
Решение.
R-1 = {(1,1), (1,3), (3,2), (4,2), (4,3)};
S-1 = {(1,1), (1,2), (1,3), (2,1), (2,4)};
S º R = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)};
(S º R)-1 = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)};
R-1 º S-1 = {(1,1), (1,2), (1,3), (2 ,1), (2,2), (2,3)} = (S º R)-1.
Задача 3.5. Пусть R отношение «...родитель...», а S отношение «...брат...» на множестве всех людей. Дайте краткое словесное описание отношениям:
R-1, S-1, R º S, S-1 º R-1 и R º R.
Решение.
R-1 - отношение«...ребёнок...»;
S-1 - отношение«...брат или сестра...»;
R º S - отношение «...родитель...»;
S-1 º R-1 - отношение «...ребёнок...»
R º R - отношение «...бабушка или дедушка...»
Задачи для самостоятельного решения
1) Пусть R - отношение «...отец...», а S - отношение «...сестра...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, R º S, S-1 º R-1, R º R.
2) Пусть R - отношение «...брат...», а S - отношение «...мать...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, S º R, R-1º S-1, S º S.
3) Пусть R - отношение «...дед...», а S - отношение «...сын...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, R º S, S-1 º R-1, S º S.
4) Пусть R - отношение «...дочь...», а S - отношение «...бабушка...» на множе- стве всех людей. Дайте словесное описание отношениям:
R-1, S-1, S º R, R-1 º S-1, R º R.
5) Пусть R - отношение «...племянница...», а S - отношение «...отец...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, S º R, R-1 º S-1, R º R.
6) Пусть R - отношение «сестра...», а S - отношение «мать...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, R º S, S-1 º R-1, S º S.
7) Пусть R - отношение «...мать...», а S - отношение «...сестра...» на множе- стве всех людей. Дайте словесное описание отношениям:
R-1, S1, R º S, S1 º R1, S º S.
8) Пусть R - отношение «...сын...», а S - отношение «...дед...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, S º R, R-1 º S-1, R º R.
9) Пусть R - отношение «...сестра...», а S - отношение «...отец...» на множе- стве всех людей. Дайте словесное описание отношениям:
R-1, S-1, R º S, S-1 º R-1, S º S.
10) Пусть R - отношение «...мать...», а S - отношение «...брат...» на множестве всех людей. Дайте словесное описание отношениям:
R-1, S-1, S º R, R-1 º S-1, R º R.