Переименования и подстановки

Роль свободных и связанных переменных. Переименование. Коллизия переменных при переименовании. Отношение конгруэнтности (≈). Подстановка, свободная для данного выражения. Сохранение конгруэнтности при подстановке. Свойство чистоты переменных. Лемма о чистоте переменных.

С понятием связанной переменной мы встречаемся уже в курсе математического анализа Обозначения предела, определенного интеграла дают примеры связывания переменных. Из того же курса известно, что связанную переменную можно изменять, не меняя смысла выражения. Однако это в общем верное правило может приводить к неверным результатам. Например, если в выражении заменить связанную переменную x переменной y, получим формулу , имеющую совсем другой смысл. В этом случае говорят, что при подстановке произошла коллизия переменных. Одновременная замена всех вхождений переменной x в кванторной приставке* ∇x и в области действия этой приставки на переменную y того же сорта называется переименованием. Коллизия переменных при переименовании в формуле ∇xX — ситуация, когда при переименовании переменной x в переменную y в X или в одной из ее подформул есть переменная, которая из свободной превращается в связанную. Например, в формуле ∀xp(x,y,z) переменные y и z являются свободными. Но при переименовании x в y получим ∀ y p (y, y, z), где только одна переменная z осталась свободной. Может быть и другая ситуация. В формуле ∀ x p₁(x, (∀y p₂ (x, y)), z) оба вхождения переменной y связанные. Переменная x в формулу входит связанно (раз есть квантор), но в подформулу∀ y p₂(x, y) эта переменная уже входит свободно. Но переименование x в y переводит y в разряд связанной переменной в этой подформуле: ∀ y p₁(y,(∀y p₂(y,y)),z). В этом случае также произошла коллизия переменных. Можно сказать по-другому. Назовем переменную x в формуле Z свободной переменной для переменной y, если никакие вхождения y в Z, являющиеся свободными для Z или одной из ее подформул, не попадают в область действия кванторных приставок с переменной x. Коллизия переменных при переименовании — попытка заменить кванторную переменную x на y в то время как x не является свободной для y. Мы будем говорить, что две формулы X и X' конгруэнтны (являются вариантами одна другой, обозначение X ≈ X'), если одна получена из другой с помощью правильного, т.е. без коллизии переменных, переименования. Точное определение этого понятия можно дать индукцией по построению формулы:

1) элементарная формула конгруэнтна только себе самой;

2) если Y ≈ Y 0, Z ≈ Z 0, то ¬Y ≈¬Y 0 и Y ∇ Z ≈ Y 0 ∇ Z 0, где ∇ — одна из трех двуместных логических связок;

3) если X = ∇xY , X0 = ∇y Z, то X ≈ X0, если x и y одного сорта и для любой переменнойz того же сорта, вообще не входящей ни в Y , ни Z, имеем Y _z ^x ≈ Z_z^y , где W_u^v есть результат замены в W всех свободных вхождений переменной v на переменную u.

Отметим, что конгруэнтность — это отношение эквивалентности (симметричное, рефлексивное и транзитивное). Таким образом, множество всех формул разделяется на классы попарно конгруэнтных формул. Хотя формально конгруэнтные формулы различаются, нет оснований такое различие учитывать. С математической точки зрения здесь осуществляется переход от понятия " формула" к более общему понятию " класс конгруэнтных формул".

Под подстановкой θ мы будем понимать символическую запись вида

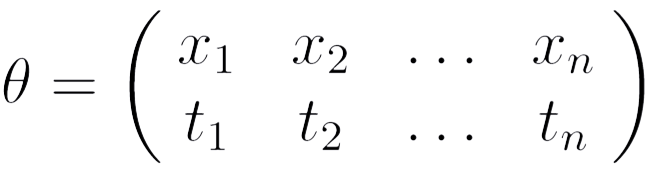
в которой x₁, x₂, ..., x_n, — конечный набор (предметных) переменных, а t₁, t₂, ..., t_n — набор термов, причем сорт терма t_i совпадает с сортом переменной x_i. Такую запись мы всегда можем трактовать как запись отображения, определенного на конечном подмножестве множества всех предметных переменных языка, в множество Tm всех термов языка, которое сохраняет сортность термов. Допускается, что приведенная таблица может быть пустой.

Далее через Tθ будем обозначать результат подстановки θ в выражение (т.е. терм или формулу) T, т.е. результат замены в T всех свободных вхождений каждой переменной x_i из подстановки θ соответствующим термом t_i,. Отметим, что при этом некоторые переменные xi могут не входить свободно в T. В этом случае в отношении x_i не происходит никаких замен, соответствующий столбец в подстановке θ можно опустить.

В алгебре высказываний подстановка — один из способов преобразования формулы в эквивалентную. При этом на подстановку не накладывалось никаких ограничений. Ситуация меняется с появлением кванторов. При подстановке в формуле с кванторами смысл формулы может заметно измениться. Поэтому не все подстановки пригодны с точки зрения логики. Например, формула** x + y = z с натуральными переменными x, y, z есть предикат от трех переменных. Формула ∃y (x+y = z) есть предикат уже от двух переменных x и z, логическим эквивалентом которого является формула x < z. Заменим в этой формуле свободную переменную x термом x·y, надеясь на то, что получим предикат x·y < z. Однако формула ∃y (x·y + y = z) имеет совсем другой смысл. Здесь возникла та же проблема, что и при переименовании — коллизия переменных: при замене переменной x термом x·y переменная y, входящая в терм свободно, оказалась в области действия кванторной приставки и стала связанной. Чтобы избежать искажения, достаточно было предварительно " убрать" из формулы связанную переменную y с помощью переименован ия а уж затем выполнить подстановку: ∃u(x·y + u = z). При таком порядке действий действительно получим предикат x·y < z.

Подстановку θ назовем свободной для выражения T, если для любой переменной x из области определения domθ подстановки θ (т.е. встречающейся в первой строке матрицы), никакое свободное вхождение x в T не попадает в область действия никаких кванторных приставок с переменными, свободно входящими в θ(x). В частности, если ни один из параметров формул θ(x) не является кванторной переменной в T, то θ свободна для T. Это будет так в случае, когда каждая из формул ϑ(x) вовсе не имеет параметров, т.е. является замкнутой. Такая подстановка называется константной.

Если подстановка θ не является свободной для T, то, как показывает рассмотренный выше пример, можно, не меняя логической сути формулы, выполнить переименование переменных в T, переходя к конгруэнтной формуле T', для которой θ уже будет свободной. Этот подход позволяет обеспечить универсальность подстановки, но, правда, пожертвовав однозначностью: результат будет лишь с точностью до когруэнтности.

Теорема 4.1. Если X' ≈ X'', а θ свободна для X' и X'', то X'θ ≈ X''θ.

◀ Доказательство базируется на индукции по построению формулы и на индуктивном определении конгруэнтности. Если X' ≈ X'', то формулы X либо обе элементарные, либо обе получены с помощью логической связки, либо обе построены присоединением кванторной приставки. В первом случае X' и X'' совпадают, а значит, формулы X'θ и X''θ также элементарны и совпадают, т.е. X' ≈ X''.

Пусть, например, X' = U'∨V ' и X'' = U''∨V '', причем U' ≈ U'', V ' ≈ V ''. По индуктивному предположению U' θ ≈ U'' θ и V 'θ ≈ V ''θ. Следовательно, U' θ ∨ V' θ ≈ U'' θ ∨ V'' θ и X' θ = (U' ∨ V ') θ = U' θ ∨ V ' θ ≈ U'' θ ∨ V ''θ = (U''∨V '')θ = X''θ.

Аналогичны рассуждения для других логических связок. Пусть X' = ∇xU', X'' = ∇yU''. Выберем переменную z, не входящую ни в формулы U', U'', ни в формулы подстановки θ. Тогда, согласно условию X' ≈ X'', имеем (U')^xz ≈ (U'')^yz. Согласно индуктивному предположению, (U')^xz θ ≈ (U'')^yz θ. Удалим из θ столбцы с переменными x и y, если они есть. Получим подстановку θ. В области значений этой подстановки переменные x и y не встречаются, поскольку θ, как и θ, свободна для X' и X''. Из равенства (U')^xz θ ≈( U'')^yz θ вытекает (U')^xz θ ≈ (U'')^yz θ, а так как (U')^xz θ = (U'θ)^xz и (U'')^yz θ = (U''θ)^yz, то (U'θ)^xz ≈ ( U''θ)^yz. Следовательно, ∇x(U'θ) = ∇y(U''θ) и ∇ x (U'θ) = ∇ y (U''θ), потому что под квантором кванторная переменная все равно не заменяется. ▶

Будем говорить, что формула X обладает свойством чистоты переменных, если, во-первых, никакая переменная кванторной приставки не входит в X свободно, и во-вторых, разные кванторные приставки содержат разные переменные. Следующая лемма позволяет утверждать, что в любой формуле T можно устроить переименование, в результате которого данная подстановка θ станет свободной для переименованной формулы.

Лемма 4.1 (о чистоте переменных). Для любой формулы X и любого множества S переменных существует формула Y , когруэнтная X, обладающая свойством чистоты переменных, в которой нет связанных переменных, принадлежащих S.

◀ Доказательство проводится индукцией по построению формулы. Для атомарных формул утверждение тривиально, поскольку такие формулы вообще не имеют связанных переменных. Пусть задано множество S и формула X = Y∇Z, где ∇ — одна из двуместных логических связок. Предположим, что относительно формул Y и Z уже доказано утверждение леммы с произвольным множеством S. Пусть S_X — множество всех переменных (и свободных, и связанных), входящих в X. Существует формула Y ', конгруэнтная Y , обладающая свойством чистоты переменных и не имеющая связанных переменных из множества S ∪SX. Обозначим через S_Y множество всех переменных, входящих в Y '. Существует формула X', конгруэнтная X, обладающая свойством чистоты переменных и не имеющая связанных переменных из множества S ∪S_Y . Формула X'∇Y ' обладает свойством чистоты переменных (любая кванторная переменная, например, в X0 не совпадает со " своими" переменными, т.е. другими кванторными переменными формулы X', а по построению и с " чужими" переменными, составляющими множество S_Y ). Кроме того, в построенной формуле нет связанных переменных, попадающих в S. Для одноместной связки ¬ утверждение теоремы очевидно.

Пусть X = ∇xY , где ∇ — один из кванторов. Сперва надо "вывести" новую кванторную переменную за пределы S. Для этого выбираем новую переменную u, не принадлежащую S и не входящую никаким образом в Y . Подстановка(x ^uz )свободна и мы получаем формулу ∇uY ^xu , конгруэнтную X. Если мы теперь заменим Y ^xu конгруэнтной формулой Y ' со свойством чистоты переменных и без переменных из S, то получим конгруэнтную Y формулу ∇uY ' со свойством чистоты переменных и без переменных из S. ▶

В соответствии с доказанной леммой, чтобы выполнить в X правильную подстановку θ, необходимо переименовать X в X' так, что среди переменных X' не будут встречаться переменные термов θ(x). Тогда подстановка θ будет свободной для X', и мы можем реализовать эту подстановку.